МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 17 (7 марта 2015 года)

1.

На прошлом занятии мы доказали, что сумма всех чисел от 1 до 2014 нечётна. Давайте теперь будем складывать только нечётные числа, от 1 до 2015: 1 + 3 + 5 + ... + 2013 + 2015. Чётна или нечётна их сумма?

2.

а) Существуют ли два натуральных числа, сумма и произведение которых нечётны? б) А три таких числа?

3.

Каждый шестиклассник принёс с собой одну или несколько тетрадей в клеточку (в тетради либо 12, либо 18, либо 48 листов) и так случилось, что внутри каждой тетради все страницы одинаковые, хотя в разных тетрадках они могут быть и разными. Кирилл решил посчитать все клеточки, какие только есть у шестиклассников, и у него получилось 12072015 клеточек. Не ошибся ли Кирилл?

4.

Филя и Степашка по очереди записывают любые натуральные числа в клетки квадрата 13×13. Начинает Степашка. Когда квадрат заполнится, подсчитывают сумму всех чисел. Если получается чётное число, выигрывает Степашка, если нечётное — Филя. У кого из них есть выигрышная стратегия?

5.

Барон Мюнхгаузен, вернувшийся из кругосветного путешествия, рассказывает, что по пути он пересёк границы Трапезундии 13 раз. Верите ли вы ему?

6.

В строку записаны 10 чисел, причём сумма любых трёх подряд стоящих чисел чётна. Может ли сумма всех десяти чисел быть нечётной?

7.

Перед гномом лежат три кучки бриллиантов: 4, 5 и 6 штук. В одной из кучек лежит один фальшивый бриллиант. Все бриллианты имеют одинаковый вид, все настоящие бриллианты весят одинаково, а фальшивый отличается от них по весу. У гнома есть чашечные весы без гирь. Гному надо за одно взвешивание найти какую-нибудь одну кучку, в которой все бриллианты наверняка настоящие. Как это сделать?

8.

Есть 26 кусочков сахара массой 1, ..., 26 г. Можно ли разделить сахар поровну между а) 13-ю; б) четырьмя; в) девятью сладкоежками?

Задачи на дом

9.

Маша говорит, что знает четыре числа, сумма и произведение которых — нечётные числа. Права ли Маша?

10.

Витя выложил из карточек с цифрами пример на сложение и затем поменял местами две карточки. Как видите, равенство нарушилось. Какие карточки переставил Витя? Можно ли это определить точно?

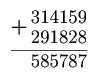
11.

Покрасьте клетки доски 5×5 в пять цветов так, чтобы в каждом горизонтальном ряду, в каждом вертикальном ряду и в каждом выделенном блоке встречались все цвета.