МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 16 (28 февраля 2015 года). Чётность

1.

Если сложить все натуральные числа от 1 до 2014, то чётной или нечётной будет сумма?

2.

В ряд стоят числа от 1 до 10. Между ними расставляют 10 знаков « + » и « − » (в том числе, « + » или « − » перед единицей), а затем вычисляют результат.

а)

Можно ли получить 61?

б)

Можно ли получить 35?

в)

Можно ли получить 7?

г)

Можно ли получить 0?

д)

Можно ли получить 1?

е)

Можно ли получить 8?

3.

Филя пишет на доску одно целое число, а Степашка — другое. Если произведение чётно, побеждает Филя, если нечётно, то Степашка. Может ли один из игроков играть так, чтобы непременно выиграть?

4.

Не выполняя никаких арифметических действий, назовите чётность чисел:

а)

\(1000 - 947 \cdot 7567 \cdot 76 + 2015 + 2016\);

б)

\(204 \cdot 2121 + 5360 \cdot 7 + 3121 + 6731 \cdot 81 \cdot 11 - 154 - 77 + 87\);

в)

\((12454651 - 4564645)\cdot (67876 - 59681) + (1163 - 712) \cdot (948 - 8569) + 886541\cdot 735+1\).

5.

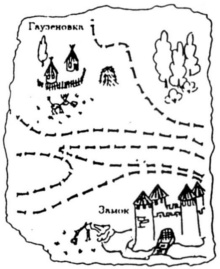Давным-давно барон Мюнхгаузен обнес свои владения забором и нарисовал на карте. Забор изображен несамопересекающейся замкнутой ломаной, внутри которой — владения барона. Барон забыл, входит ли в его владения деревня Гаузеновка. Он смог найти лишь обрывок карты, на который попали его замок, деревня Гаузеновка и часть забора, проходящая по этому участку. (Как проходит забор за границами карты, неизвестно.) Как выяснить, входит ли деревня во владения барона?

6.

Можно ли разменять 25 рублей при помощи десяти купюр достоинством в 1, 3 и 5 рублей?

7.

Имеются гири массой а) 1, 2, ..., 20 г; б) 1, 2, ..., 21 г. Можно ли их разбить на несколько групп так, чтобы в каждой группе самая тяжелая гиря уравновешивала все остальные?

8.

Есть 101 монета, из которых 50 фальшивых. Фальшивая монета на 1 грамм тяжелее настоящих. Петя взял одну монету и за одно взвешивание на весах со стрелкой, показывающей разность весов на чашках, хочет определить, фальшивая ли она. Сможет ли он это сделать?

Задачи на дом

9.

Можно ли доску размером 5×5 заполнить доминошками размером 1×2?

10.

Первоклассник Петя знает только нечётные цифры. Он написал три пятизначных числа. Его старший брат сложил эти числа. Могло ли получиться, что Петя а) не знает ни одну из цифр получившейся суммы? б) знает только одну из цифр получившейся суммы?

11.

Можно ли из фигурок и сложить квадрат, используя фигурки обоих видов? Фигурки можно поворачивать и переворачивать.

12.

На доске записано число 123456789. У написанного числа выбираются две соседние цифры, если ни одна из них не равна 0, из каждой цифры вычитается по 1, и выбранные цифры меняются местами (например, из 123456789 можно за одну операцию получить 123436789). Какое наименьшее число может быть получено в результате таких операций?