МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 11 (6 декабря 2014 года)

1.

Катя и её друзья встали в круг. Оказалось, что оба соседа каждого ребёнка — одного пола. Среди Катиных друзей пятеро мальчиков. А сколько девочек?

2.

Подберите числа x, y и z так, чтобы выполнялось равенство 28x + 30y + 31z = 365.

3.

Между 9 планетами Солнечной системы введено космическое сообщение. Ракеты летают по следующим маршрутам: Земля — Меркурий, Плутон — Венера, Земля — Плутон, Плутон — Меркурий, Меркурий — Венера, Уран — Нептун, Нептун — Сатурн, Сатурн — Юпитер, Юпитер — Марс и Марс — Уран. Можно ли добраться с Земли до Марса?

4.

Однажды утром кто-то принес букет цветов и поставил его вазу на учительском столе. Когда ребята собрались, учительница спросила: „А знаете ли вы, кто принес цветы?” Ребята стали гадать. Были высказаны предположения: цветы принесли Андрей и Борис, Андрей и Даша, Андрей и Сергей, Борис и Даша, Борис и Володя, Володя и Галя, Галя и Даша. Учительница сказала, что в одном из этих предположений одно имя названо правильно, а второе — неправильно. Во всех же остальных предположениях оба имени названы неправильно. Кто принес цветы?

5.

На день рождения к Андрею пришли Вася, Глеб, Даша, Митя, Петя, Соня и Тимур. Покажите, как восьмерых ребят можно рассадить за круглый стол, чтобы у любых двух, сидящих рядом, в именах встречались одинаковые буквы.

6.

Мама купила кускового сахара. Дети сначала съели верхний слой — 77 кусков, затем боковой слой — 55 кусков, наконец, передний слой. Сколько кусочков сахара осталось в коробке?

7.

В некотором государстве каждый город соединен с каждым дорогой. Сумасшедший король хочет ввести на дорогах одностороннее движение так, чтобы, выехав из любого города, в него нельзя было вернуться. Можно ли так сделать? (Возможно, что после этого из некоторых городов будет вообще нельзя выехать.)

Задачи на дом

8.

Трое друзей принесли с собой на Малый мехмат конфеты. Первый отдал каждому из остальных столько конфет, сколько у того уже было. Затем остальные по очереди сделали то же самое. После этого конфет у них стало поровну. Сколько всего конфет ребята принесли на Малый мехмат, если первый принёс 13 конфет?

9.

Среди четырёх людей нет трёх с одинаковым именем, или с одинаковым отчеством, или с одинаковой фамилией, но у каждых двух из них совпадает или имя, или отчество, или фамилия. Может ли такое быть?

10.

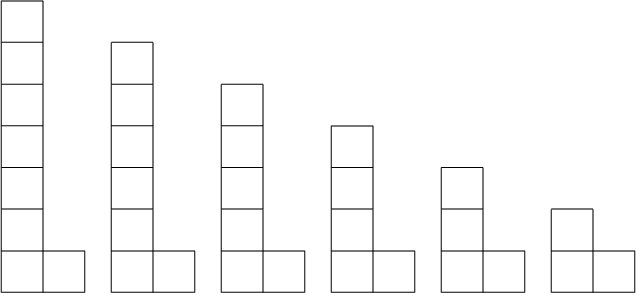
Соберите прямоугольник из уголков, изображённых на рисунке. Каждый уголок нужно использовать ровно один раз.