МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 6 (1 ноября 2014 года)

0.

Кузнечик путешествует по числовой прямой. Вправо он умеет прыгать только ровно на 3 см, а влево — только ровно на 5 см. Как Кузнечику сместиться ровно на а) 11 см влево; б) 1000 см влево; в) 1 см вправо; г) 2014 см влево; д) 2014 см вправо?

В этом листочке некоторые задачи посвящены переливаниям разных жидкостей. За одно переливание из одного сосуда в другой можно либо вылить всё, что есть в первом сосуде, либо долить второй сосуд до краёв.

1.

Есть два ведра: одно ёмкостью 4 л, другое — 9 л. Можно ли только с их помощью набрать из реки а) ровно 3 л воды; б) ровно 6 л воды?

2.

Можно ли набрать из реки 8 л воды с помощью двух вёдер вместимостью 15 л и 16 л?

3.

Есть три кастрюли: 8 л — с компотом, 3 л и 5 л — пустые. Как разделить компот пополам? (Компот, в отличие от воды, выливать нельзя.)

4.

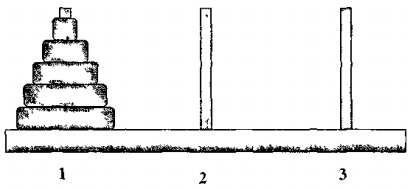
Ханойские башни. Есть три стержня и несколько колец разного размера. Класть можно только меньшее кольцо на большее. Как переместить составленную из колец пирамидку с одного стрежня на другой, если в пирамидке: а) 3 кольца; б) 5 колец?

5.

Дан мешок сахарного песка, чашечные весы и гирька в 1 г. Как

а)

за 2 взвешивания отмерить 3 г сахара?

б)

за 4 взвешивания отмерить 10 г сахара?

в)

за 10 взвешиваний отмерить 1 кг сахара?

6.

Есть двое песочных часов: на 7 мин и на 11 мин. Каша варится 15 мин. Как с помощью этих часов отмерить нужное время?

7.

Есть три сосуда 3 л, 4 л и 5 л, кран с водой и 3 л сиропа в самом маленьком сосуде. Можно ли с помощью переливаний получить 6 л смеси воды с сиропом так, чтобы в каждом сосуде воды и сиропа было поровну?

Задачи на дом

8.

В ведро налили 12 литров молока. Пользуясь лишь сосудами в 5 и 7 литров, разделите молоко на две равные части.

9.

Можно ли разлить 50 л бензина по трём бакам так, чтобы в первом баке было на 10 литров больше, чем во втором, а во втором на 21 литр больше, чем в третьем?

10.

В нескольких стаканах достаточно большой вместимости налито поровну воды. Разрешается переливать из любого стакана в любой другой столько воды, сколько имеется в этом последнем. Можно ли за конечное число шагов слить воду в один стакан, если стаканов а) 4? б) 5? в) 6? г) 32?

11.

За круглым столом сидят 4 гнома. Перед каждым стоит кружка с молоком. Один из гномов переливает ¹/₄ своего молока соседу справа. Затем сосед справа делает то же самое. Затем то же самое делает следующий сосед справа и наконец четвёртый гном ¹/₄ оказавшегося у него молока наливает первому. Во всех кружках вместе молока 2 л. Сколько молока было первоначально в кружках, если в конце у всех гномов молока оказалось поровну?