МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 2 (4 октября 2014 года)

1.

Алёша задумал число. Он прибавил к нему 5, потом разделил сумму на 3, умножил на 4, отнял 6, разделил на 7 и получил число 2. Какое число задумал Алёша?

2.

На озере расцвела белая лилия. Каждый день число её цветков удваивалось, а на 20-й день всё озеро покрылось цветами. На который день покрылась цветами половина озера?

3.

Два пирата играли на золотые монеты. Сначала первый проиграл половину своих монет (отдал второму), потом второй проиграл половину своих, потом снова первый проиграл половину своих. В результате у первого оказалось 15 монет, а у второго — 33. Сколько монет было у первого пирата до начала игры?

4.

Над цепочкой озёр летели гуси. На каждом садилась половина подлетевших к этому озеру гусей и ещё полгуся, а остальные летели дальше. Все гуси сели на 7 озёрах. Сколько было гусей?

5.

На окружности стоят 6 фишек белого и чёрного цветов. Настя убрала все белые фишки, у которых есть хотя бы один чёрный сосед. После этого Алёша убрал все чёрные фишки, у которых есть хотя бы один белый сосед. Могла ли после этого на окружности остаться одна фишка? Если да — то какого она цвета?

* * *

6.

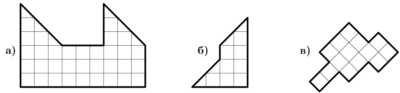
Разрежьте каждую из фигур на 2 равные части:

7.

Квадрат 4×4 раскрашен так, как показано на рисунке справа. За один ход разрешается выбрать любой прямоугольник и внутри него изменить все цвета на противоположные. В три хода добейтесь, чтобы квадрат был раскрашен в шахматном порядке.

8.

На столе лежат 12 конфет. Двое игроков (Петя и Вася) по очереди съедают конфеты. За ход можно съесть одну или две конфеты. Если игрок не может пойти (т.е. конфет не осталось), то он проиграл. Первым ходит Петя. Кто из игроков может гарантированно выиграть? Объясните, как ему нужно для этого играть.

Задачи на дом

9.

а)

Расставьте в примере 100 − 20 × 3 + 2 скобки всеми возможными способами.

б)

Укажите наибольший и наименьший результат.

10.

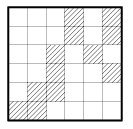
Разрежьте изображённую на рисунке доску на четыре одинаковые части, чтобы каждая из них содержала три заштрихованные клетки.

11.

Отметьте на доске 8×8 несколько клеток так, чтобы любая (хоть отмеченная, хоть неотмеченная) клетка граничила по стороне ровно с одной отмеченной клеткой.