МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 24 (25 апреля 2015 года)

1.

Дан куб с ребром 2. Покажите, как наклеить на него без наложений 10 квадратов со стороной 1 так, чтобы никакие квадраты не граничили по отрезку (по стороне или её части). Перегибать квадраты нельзя.

2.

В музее Гуггенхайма в Нью-Йорке есть скульптура, имеющая форму куба. Жук, севший на одну из вершин, хочет как можно быстрее осмотреть скульптуру, чтобы перейти к другим экспонатам (для этого достаточно попасть в противоположную вершину куба).

а)

Какой путь ему выбрать?

б)

Сколькими способами он может это сделать?

3.

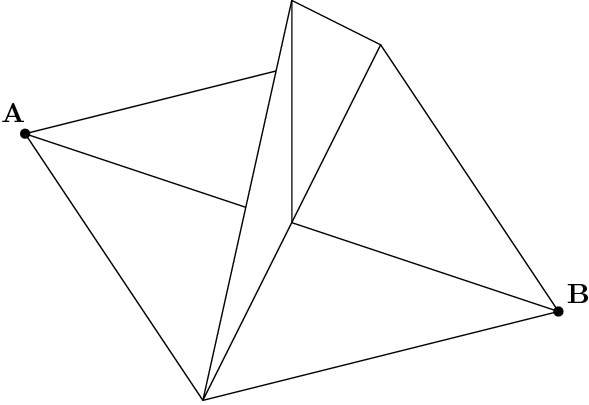
В вершине A квадрата со стороной 10 см сидит муравей. Ему надо добраться до диаметрально противоположной вершины B, где находится вход в муравейник. Вдоль другой диагонали построена треугольная стена, боковые стороны которой тоже равны 10 см. Найдите длину кратчайшего пути, который надо преодолеть муравью, чтобы попасть в муравейник.

4.

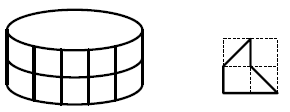
Полина решила раскрасить свой клетчатый браслет размером 10×2 (на рисунке слева) узором из одинаковых фигурок (на рисунке справа), чередуя в них два цвета (так, чтобы фигурки, имеющие общий участок границы, были разного цвета). Как ей это сделать?

5.

Из бумаги склеено цилиндрическое кольцо, ширина которого равна 1, а длина по окружности равна 4. Можно ли, не разрывая, сложить это кольцо так, чтобы получился квадрат площади 2?

6.

В некотором государстве города соединены дорогами. Длина каждой дороги меньше 500 км, и из каждого города в любой другой можно попасть, проехав по дорогам меньше 500 км. Когда одна дорога оказалась закрытой на ремонт, выяснилось, что из каждого города можно проехать по оставшимся дорогам в любой другой. Докажите, что при этом можно проехать меньше 1500 км.

Дополнительные задачи

7.

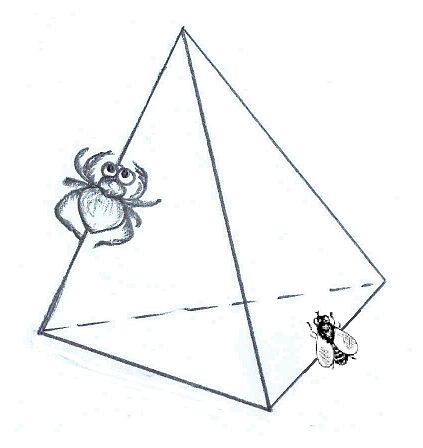
На середине ребра тетраэдра сидит паук, а на середине противоположного ребра — муха. Как пауку добраться до мухи по кратчайшему пути?

8.

В лесу растут деревья с квадратными стволами. Связисту нужно протянуть провод из точки A в точку B, расстояние между которыми равно 100 м. Хватит ли ему для этой цели куска провода длиной 200 м?

9.

На кольцевой автомобильной дороге стоят несколько одинаковых автомашин. Если бы весь бензин, имеющийся в этих автомашинах, слили в одну, то эта машина смогла бы проехать по всей кольцевой дороге и вернуться на прежнее место. Докажите, что хотя бы одна из этих машин может объехать всё кольцо, забирая по пути бензин у остальных машин.