МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 17 (7 марта 2015 года)

1.

Аборигены поймали Кука и просят за него выкуп в 455 рупий пятьюдесятью монетами достоинств 5, 17 или 31 рупия. Можно ли выкупить Кука на таких условиях?

2.

А если бы они хотели получить сумму 910 рупий пятьюдесятью монетами по 10, 34 и 62 рупии?

3.

Шестиклассник вычел из простого числа простое число и получил 2015. Какие числа он вычитал друг из друга?

4.

За круглым столом сидят 30 человек — рыцари и лжецы (рыцари всегда говорят правду, а лжецы всегда лгут). Известно, что у каждого из них за этим же столом есть ровно один друг, причем у рыцаря этот друг — лжец, а у лжеца этот друг — рыцарь (дружба всегда взаимна). На вопрос „Сидит ли рядом с вами ваш друг?” сидевшие через одного ответили «да». Сколько из остальных могли также ответить «да»?

5.

Дети перебрасываются красными, белыми и синими мячами. Каждый ребенок бросил и поймал в сумме три мяча, причем это мячи различных цветов. Кроме того, некоторые три мяча были брошены, но никем не пойманы. Докажите, что эти три мяча — трёх различных цветов.

6.

Когда встречаются два жителя Цветочного города, один отдает другому монету в 10 копеек, а тот ему — 2 монеты по 5 копеек. Могло ли случиться так, что за день каждый из 2015 жителей города отдал ровно 10 монет?

7.

Может ли прямая пересекать все стороны а) 2014-угольника; б) 2015-угольника, если она не проходит через его вершины?

8.

Прямоугольник разрезали шестью вертикальными и шестью горизонтальными разрезами на 49 прямоугольников (см. рисунок). Оказалось, что периметр каждого из получившихся прямоугольников — целое число метров. Обязательно ли периметр исходного прямоугольника — целое число метров?

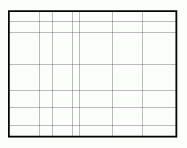
9.

По кругу расставлены 15 натуральных чисел. Докажите, что можно выкинуть два соседних числа так, что оставшиеся числа нельзя разбить на две группы с равной суммой.

Задачи на дом

10.

Есть 99 палочек с длинами 1, 2, 3, ..., 99. Можно ли из них сложить контур какого-нибудь прямоугольника?

11.

Найдите все простые числа, которые нельзя записать в виде суммы двух составных.