МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 21 (4 апреля 2015 года)

1.

Охотник рассказал приятелю, что видел в лесу волка с метровым хвостом. Тот рассказал другому приятелю, что в лесу видели волка с двухметровым хвостом. Передавая новость дальше, простые люди увеличивали длину хвоста вдвое, а творческие — втрое. В результате по телевизору сообщили о волке с хвостом длиной 648 метров. Сколько простых и сколько творческих людей «отрастили» волку хвост?

2.

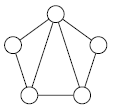
Впишите в пять кружков на рисунке натуральные числа так, чтобы выполнялись два условия: 1) если два кружка соединены линией, то стоящие в них числа должны отличаться ровно в два или ровно в четыре раза; 2) если два кружка не соединены линией, то отношение стоящих в них чисел не должно быть равно ни 2, ни 4.

3.

У нескольких крестьян есть 128 овец. Если у кого-то из них оказывается не менее половины всех овец, остальные сговариваются и раскулачивают его: каждый берёт себе столько овец, сколько у него уже есть. Если у двоих по 64 овцы, то раскулачивают кого-то одного из них. Произошло 7 раскулачиваний. Докажите, что все овцы собрались у одного крестьянина.

4.

Первоклассник учится чистописанию по следующей системе: в день начала обучения он написал одну букву, а в каждый следующий день он пишет вдвое больше букв, чем писал в предыдущий день. Что больше и на сколько: число букв, которое он напишет завтра, или общее число букв, которое написал до сегодняшнего дня включительно?

5.

Расставьте в клетках таблицы 3×3 числа 2, 4, 8, 16, 32, 64, 128, 256 и 512 так, чтобы произведения по всем вертикалям, горизонталям и обеим большим диагоналям были равны.

6.

Малыши играют в «магазин». Они нарисовали всего шесть купюр, каждая достоинством в некоторое целое число рублей. Оказалось, что с помощью этого набора купюр можно заплатить без сдачи любую сумму от 1 до 63 рублей. Как им это удалось?

7.

Разрежьте по клеточкам квадрат 7×7 на девять прямоугольников (не обязательно различных), из которых можно будет сложить любой прямоугольник со сторонами, не превосходящими 7.

Дополнительные задачи

8.

Длина взрослого червяка 1 метр. Если червяк взрослый, его можно разрезать на две части в любом отношении длин. При этом получаются два новых червяка, которые сразу начинают расти со скоростью 1 метр в час каждый. Когда длина червяка достигает метра, он становится взрослым и прекращает расти. Можно ли из одного взрослого червяка получить 10 взрослых червяков быстрее, чем за час? (задача уже давалась в допе осенью, ну и ладно)

9.

Летела стая гусей. На каждом озере садилась половина гусей и еще полгуся. Остальные летели дальше. Все гуси сели на 100 озёрах. Сколько всего гусей было в стае?

10.

Можно ли в таблицу 4×4 расставить такие натуральные числа, что одновременно выполняются следующие условия:
1) произведения чисел, стоящих в одной строке, одинаковы для всех строк;
2) произведения чисел, стоящих в одном столбце, одинаковы для всех столбцов;
3) среди чисел нет равных;
4) все числа не больше 100?

11.

В королевстве 16 городов. Король хочет построить такую систему дорог, чтобы из каждого города можно было попасть в каждый, минуя не более одного промежуточного города, и чтобы из каждого города выходило не более 5 дорог.

а)

Как это сделать?

б)

Докажите, что если в формулировке заменить число 5 на число 4, то желание короля станет неосуществимым.