МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 6 (1 ноября). Математическая регата

Первый тур (10 минут, задачи по 6 баллов)

1.1

Винни-Пух вышел из гостей от Кристофера Робина на 6 минут позже Пятачка. Через какое время он догонит Пятачка, если его скорость в три раза больше скорости Пятачка?

1.2

Найдите сумму всех чётных чисел от 2 до 2002.

1.3

Из спичек сложено неверное равенство. Переложите одну спичку так, чтобы равенство стало верным.

Второй тур (15 минут, задачи по 7 баллов)

2.1

В ящике лежит 10 пар белых перчаток и 20 пар чёрных. Какое наименьшее число перчаток нужно вынуть не глядя, чтобы среди них наверняка оказались левая и правая перчатки одного цвета?

2.2

Вычислите значение произведения: 77×999...99 (2014 девяток).

2.3

Какое наибольшее число небьющих друг друга ладей можно расставить в клетках доски странной формы, изображённой на рисунке, если сквозь границы доски ладьи бить не могут?

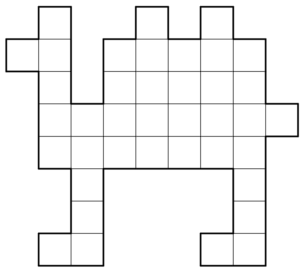
Третий тур (20 минут, задачи по 8 баллов)

3.1

Вася задумал число и прибавил к этому числу его сумму цифр. Петя также задумал число и тоже прибавил к нему его сумму цифр. В результате сложения у Васи и Пети получились одинаковые числа. Обязательно ли они задумывали одинаковые числа?

3.2

Все натуральные числа от 1 до 1000 выписали в следующем порядке: сначала были выписаны в порядке возрастания числа, сумма цифр которых равна 1, затем, также в порядке возрастания, числа с суммой цифр 2, потом — числа, сумма цифр которых равна 3 и т. д. На каком месте оказалось число 997?

3.3

В автобусе имеются одноместные и двухместные сидения. Кондуктор заметил, что когда в автобусе сидело 13 человек, то 9 сидений были полностью свободными, а когда сидело 10 человек, то свободными были 6 сидений. Сколько сидений могло быть в автобусе?

Четвёртый тур (25 минут, задачи по 9 баллов)

4.1

На физическом кружке учитель поставил следующий эксперимент. Он разложил на чашечные весы 16 гирек массами 1, 2, 3, ..., 16 грамм так, что одна из чаш перевесила. Пятнадцать учеников по очереди выходили из класса и забирали с собой по одной гирьке, причём после выхода каждого ученика весы меняли свое положение и перевешивала противоположная чаша весов. Какая гирька могла остаться на весах?

4.2

Имеется 555 гирь весом: 1 г, 2 г, 3 г, 4 г, —, 555 г. Разложите их на 3 равные по весу кучи.

4.3

Найдите все решения ребуса ТИК + ТАК = АКТ. Доказывать, что других решений нет, не требуется.