МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 5 (25 октября 2014 года)

1-й листок

1.

Чебурашка выписал все числа от 1 до 1000000. И задумался, что больше: сумма всех нечётных чисел или сумма всех чётных чисел (среди выписанных), и на сколько. Скорее помогите Чебурашке решить этот вопрос, пока он не принялся считать обе суммы в столбик.

2.

На столе в ряд лежат четыре монеты. Среди них обязательно есть как настоящие, так и фальшивые (которые легче настоящих). Известно, что любая настоящая монета лежит левее любой фальшивой. Как за одно взвешивание на чашечных весах без гирь определить тип каждой монеты, лежащей на столе?

3.

Быстро найдите сумму цифр в таблице:

1	9	3	7	4	6	2	8
4	6	5	5	8	2	6	4
1	7	4	3	5	6	2	1
9	3	6	7	5	4	8	9
5	3	8	1	6	3	1	2
7	5	9	2	7	4	8	9
2	5	4	7	1	8	6	3
6	3	8	5	4	7	9	2

4.

На столе лежат 9 карточек, на которых написаны натуральные числа от 1 до 9. Двое по очереди откладывают в сторону по одной карточке. Проигрывает тот, после хода которого сумма чисел на отложенных карточках станет больше 25. Кто выигрывает при правильной игре?

5.

а)

В строчку написаны 10 единиц. Петя и Вася по очереди ставят между какими-нибудь соседними числами знаки «+» или «−» (если там ещё нет знака). Начинает Петя. Когда между всеми соседними числами расставлены знаки, вычисляют значение полученного выражения. Если оно чётное, выигрывает Вася, иначе — Петя. Может ли один из ребят играть так, чтобы всегда выигрывать (как бы ни играл другой), и, если может, то как ему следует играть?

б)

А если можно ставить «+» или знак умножения? (При вычислении выражения сначала выполняются умножения, потом — сложения.)

6.

На столе стоят восемь стаканов с водой. Разрешается взять любые два стакана и уравнять в них количества воды, перелив часть воды из одного стакана в другой. Докажите, что с помощью таких операций можно добиться того, чтобы во всех стаканах было поровну воды.

7.

Одно из чисел получается из другого перестановкой цифр. Может ли их сумма равняться \(\underbrace{999\ldots 9}_\text{999 девяток}\)?

2-й листок

8.

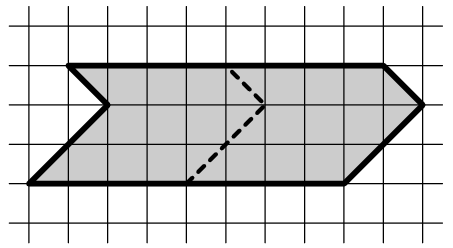
На рисунке изображена фигура, разрезанная на две равные части. Найдите ещё два способа разрезать её на равные части.

9.

На рисунке — ребус. Все цифры, обозначенные буквой Ч, — чётные (но не обязательно равные); все цифры, обозначенные буквой Н, — нечётные (тоже не обязательно равные). Расшифруйте ребус. Сколько решений он имеет?

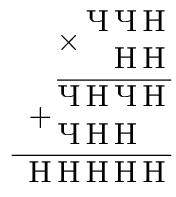
10.

В ряду из а) 2016; б) 2015 гирек вес каждой гирьки составляет целое число граммов и не превышает 1 кг. Веса любых двух соседних гирек отличаются ровно на 1 г, а общий вес всех гирь в граммах является чётным числом. Докажите, что гирьки можно разделить на две кучки, суммы весов в которых равны.

11.

Разбейте квадрат 6×6 на доминошки 2×1 и проведите в каждой из них одну из диагоналей так, чтобы ни у каких двух из этих диагоналей концы не совпадали.

12.

Двое играют на доске 19×94 клеток. Каждый по очереди отмечает квадрат по линиям сетки (любого возможного размера) и закрашивает его. Выигрывает тот, кто закрасит последнюю клетку. Дважды закрашивать клетки нельзя. Кто выигрывает при правильной игре?