МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 14 (14 февраля 2015 года). Математическая регата

Правила математической регаты

1. В составе каждой команды — 3–5 человек.
2. Соревнование проводится в четыре тура. Каждый тур представляет собой коллективное письменное решение трех задач. Каждая задача оформляется и сдается в жюри на отдельном листе. Каждая команда имеет право сдать только по одному варианту решения каждой из задач.
3. Использование какой-либо математической литературы или калькуляторов запрещено. Мобильные телефоны должны быть отключены.
4. Проверка решений осуществляется жюри после окончания каждого тура.
5. Разбор задач для учащихся осуществляется параллельно с проверкой. Итоги проверки объявляются только после окончания этого разбора. После объявления итогов тура, команды, не согласные с тем, как оценены их решения, имеют право подать заявки на апелляции.
6. Команды-победители и призеры регаты определяются по сумме баллов, набранных каждой командой во всех турах.

Первый тур (10 минут)

1.1 (6 баллов).

Саша пригласил Петю в гости, сказав, что живёт в 10-м подъезде в квартире № 333, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом девятиэтажный. На какой этаж ему следует подняться? (На каждом этаже число квартир одинаково, номера квартир в доме начинаются с единицы.)

1.2 (6 баллов).

Знайка пришёл в гости к братьям-близнецам Винтику и Шпунтику, зная, что один из них никогда не говорит правду, и спросил одного из них: «Ты Винтик?» «Да» — ответил тот. Когда Знайка спросил об этом же второго, то получил столь же чёткий ответ и сразу определил, кто есть кто. Кого звали Винтиком?

1.3 (6 баллов).

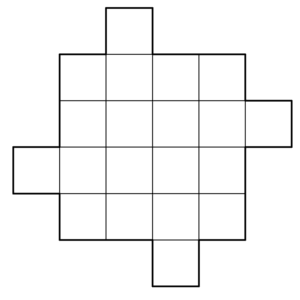
Найдите как можно больше способов разрезать изображённую на рисунке фигурку на четыре равные части. Резать можно только по линиям сетки. Способы, отличающиеся только поворотом доски, считаются одинаковыми.

Второй тур (15 минут)

2.1 (7 баллов).

Волк с тремя поросятами написал детектив «Три поросёнка-2», а потом вместе с Красной Шапочкой и её бабушкой кулинарную книгу «Красная Шапочка-2». В издательстве выдали гонорар за обе книжки поросёнку Наф-Нафу. Он забрал свою долю и передал оставшиеся 2100 золотых монет Волку. Гонорар за каждую книгу делится поровну между её авторами. Сколько денег Волк должен взять себе?

2.2 (7 баллов).

Перед гномом лежат три кучки бриллиантов: 4, 5 и 6 штук. В одной из кучек лежит один фальшивый бриллиант. Все бриллианты имеют одинаковый вид, все настоящие бриллианты весят одинаково, а фальшивый отличается от них по весу. У гнома есть чашечные весы без гирь. Гному надо за одно взвешивание найти какую-нибудь одну кучку, в которой все бриллианты наверняка настоящие. Как это сделать?

2.3 (7 баллов).

Покажите, как разрезать квадрат размером 5×5 клеток на «уголки» шириной в одну клетку так, чтобы все «уголки» состояли из разного количества клеток. Длины «сторон» уголка могут быть как одинаковыми, так и различными.

Третий тур (20 минут)

3.1 (8 баллов).

На совместной конференции партий лжецов и правдолюбов в президиум было избрано 32 человека, которых рассадили в четыре ряда по 8 человек. В перерыве каждый член президиума заявил, что среди его соседей есть представители обеих партий. Известно, что лжецы всегда лгут, а правдолюбы всегда говорят правду. При каком наименьшем числе лжецов в президиуме возможна описанная ситуация? (Два члена президиума являются соседями, если один из них сидит слева, справа, спереди или сзади от другого.)

3.2 (8 баллов).

Можно ли разрезать прямоугольник размерами 78×55 см на прямоугольники 5×11 см?

3.3 (8 баллов).

В обменном пункте совершаются операции двух типов:

1. дай 2 евро — получи 3 доллара и конфету в подарок;
2. дай 5 долларов — получи 3 евро и конфету в подарок.

Когда богатенький Буратино пришел в обменник, у него были только доллары. Когда ушёл — долларов стало поменьше, евро так и не появились, зато он получил 50 конфет. Во сколько долларов обошёлся Буратино такой «подарок»?

Четвёртый тур (20 минут)

4.1 (8 баллов).

Три человека A, B, C пересчитали кучу шариков четырёх цветов (см. таблицу). При этом каждый из них правильно различал какие-то два цвета, а два других мог путать: один путал красный и оранжевый, другой — оранжевый и жёлтый, а третий — жёлтый и зелёный. Результаты их подсчётов приведены в таблице. Сколько каких шариков было на самом деле?

	красный	оранжевый	жёлтый	зелёный
A	2	5	7	9
B	2	4	9	8
C	4	2	8	9

4.2 (8 баллов).

Айрат выписал подряд все числа месяца: 123456789101112... и покрасил три дня (дни рождения своих друзей), никакие два из которых не идут подряд. Оказалось, что все непокрашенные участки состоят из одинакового количества цифр. Докажите, что первое число месяца покрашено.

4.3 (8 баллов).

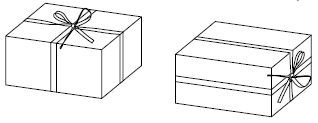
Торт упакован в коробку с квадратным основанием. Высота коробки вдвое меньше стороны этого квадрата. Ленточкой длины 156 см можно перевязать коробку и сделать бантик сверху (как на рисунке слева). А чтобы перевязать её с точно таким же бантиком сбоку (как на рисунке справа), нужна ленточка длины 178 см. Найдите размеры коробки.