МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 2 (4 октября 2014 года)

1.

На конечной станции в пустой вагон метро Цветочного города вошли несколько коротышек и сели в ряд на одну длинную лавку. На следующей станции между каждыми двумя сидевшими рядом коротышками сел ещё один коротышка. А на следующей станции снова между каждыми двумя коротышками сел один коротышка. Тут в вагон вбежал Незнайка и увидел, что все места на лавке заняты 49 коротышками. Сколько коротышек сели на лавку в начале?

2.

Преподаватель придумал несколько задач. За первые пятнадцать минут школьники решили две трети всех задач и ещё две трети задачи. За вторые пятнадцать минут — три четверти всех оставшихся задач и ещё три четверти задачи. За оставшееся время школьники дорешали все его задачи, решив половину оставшихся и ещё ползадачи. Сколько задач придумал преподаватель?

3.

С числами можно выполнять следующие операции: умножать на два или произвольным образом переставлять цифры (нельзя только ставить нуль на первое место). Можно ли с помощью таких операций из 1 получить 112?

4.

По кругу расставлены 9 нулей и единиц, причём есть как единицы, так и нули. За один ход между каждыми двумя соседними числами записывают 0 в случае, если числа равны, и 1 в противном случае. После этого старые числа стираются. Могут ли в конце все числа оказаться нулями?

5.

Костя задумал натуральное число, умножил его на 4, стёр последнюю цифру результата, умножил на 5, опять стёр последнюю цифру, умножил на 6, стёр последнюю цифру, умножил на 7, стёр последнюю цифру. Получилось число 21. Какое число мог загадать Костя?

6.

На столе лежат 12 конфет. Двое игроков (Петя и Вася) по очереди съедают конфеты. За ход можно съесть одну или две конфеты. Если игрок не может пойти (т.е. конфет не осталось), то он проиграл. Первым ходит Петя. Кто из игроков может гарантированно выиграть? Объясните, как ему нужно для этого играть.

7.

а)

Расставьте 7 звёздочек в таблице 4×4 так, чтобы при вычёркивании любых двух строк и любых двух столбцов оставалась невычеркнутой хотя бы одна звёздочка.

б)

Можно ли так расставить 6 звёздочек?

Дополнительные задачи

8.

Какое максимальное число ферзей можно расставить на доске 8×8 так, чтобы они не били друг друга?

9.

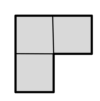
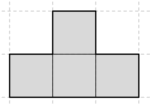
Двое играют на доске 8×8. Первый игрок выставляет на доску Т-образные фигурки из четырех клеток, а второй — уголки из трёх клеток. Проигрывает тот, кто не может сделать ход. Кто из двух игроков может обеспечить себе победу и как он для этого должен играть?

10.

За столом сидят 7 гномов, перед каждым — кружка, в некоторые налит эль (но, быть может, не поровну). Первый гном разлил весь свой эль поровну в кружки всем остальным. Затем второй разлил свой эль поровну всем остальным (включая первого), затем третий гном и т.д. до седьмого. Когда и седьмой гном разлил свой эль, у всех оказалось столько же эля, сколько было вначале. Сколько эля в каждой кружке, если всего его 3 литра?