МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 1 (27 сентября 2014 года)

1-й листок

1.

а)

Какое наибольшее количество трёхклеточных уголков можно вырезать из доски 5×5?

б)

Какое наибольшее количество четырёхклеточных букв «Т» можно вырезать из доски 5×5?

2.

В тёмной комнате стоит шкаф, в котором лежат 5 пар чёрных, 10 пар коричневых и 15 пар синих носков. Какое минимальное количество носков нужно взять из шкафа, чтобы из них заведомо можно было составить по крайней мере

а)

одну пару носков;

б)

одну пару носков коричневого цвета;

в)

две пары носков;

г)

две пары носков одного цвета;

д)

две пары носков разного цвета;

е)

две пары чёрных носков;

ё)

пять пар носков;

ж)

3 пары коричневых и 2 пары чёрных носков?

3.

Том Сойер взялся покрасить очень длинный забор, соблюдая условие: любые две доски, между которыми ровно две, ровно три или ровно пять досок, должны быть окрашены в разные цвета. Какое наименьшее количество красок потребуется Тому для этой работы?

4.

В фотоателье залетели 50 птиц — 18 скворцов, 17 трясогузок и 15 дятлов. Каждый раз, как только фотограф щёлкнет затвором фотоаппарата, какая-то одна из птичек улетит (насовсем). Сколько кадров сможет сделать фотограф, чтобы быть уверенным: у него останется не меньше 11 птиц какого-то одного вида, и не меньше десяти — какого-то другого?

5.

В ящике лежат 100 шариков белого, синего и красного цвета. Если, не заглядывая в ящик, вытащить 26 шариков, то среди них обязательно найдутся 10 шариков одинакового цвета. Какое наименьшее число шариков нужно вытащить, не заглядывая в ящик, чтобы среди них наверняка нашлись 30 шариков одинакового цвета?

2-й листок

6.

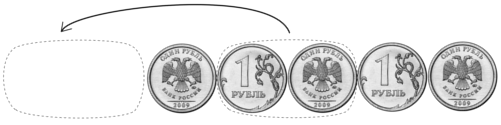
На столе лежат пять одинаковых монет. Три из них лежат орлом, две — решкой кверху, в следующем порядке: орёл, решка, орёл, решка, орёл (как на верхнем рисунке). За один ход разрешается передвинуть любые две касающиеся друг друга монеты на любое свободное место в том же ряду, не сдвигая при этом других монет и не меняя перемещаемые монеты местами. За несколько таких ходов поставьте монеты так, как показано на нижнем рисунке: орёл, орёл, орёл, решка, решка.

7.

Разложите 100 орехов на 10 кучек так, чтобы в них было разное количество орехов, но никакую из кучек нельзя было разбить на две так, чтобы число орехов во всех 11 кучках оставалось различным.

8.

Даны 103 монеты одинакового внешнего вида. Известно, что две из них — фальшивые, что все настоящие одинакового веса, что фальшивые — тоже одинакового веса, отличающегося от веса настоящих монет. Но неизвестно, в какую сторону отличаются веса фальшивых монет от настоящих. Как можно это узнать с помощью трёх взвешиваний на двухчашечных весах без гирь? (Выявлять фальшивые монеты не требуется.)