МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 4 (18 октября 2014 года)

1-й листок

1.

На острове Контрастов живут и рыцари, и лжецы. Рыцари всегда говорят правду, лжецы всегда лгут. Некоторые жители заявили, что на острове чётное число рыцарей, а остальные заявили, что на острове нечётное число лжецов. Может ли число жителей острова быть нечётным?

2.

Три коржика тяжелее пяти пирожков.

а)

Могут ли пять коржиков быть легче семи пирожков?

б)

Могут ли семь коржиков быть легче тринадцати пирожков?

3.

Чебурашка нарисовал несколько клетчатых фигур и задумался, чётно или нечётно число клеточек в каждой из них. Взгляните на рисунки и поскорее ответьте на Чебурашкин вопрос, пока он не принялся считать клеточки в этих фигурах!

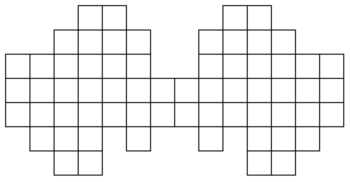
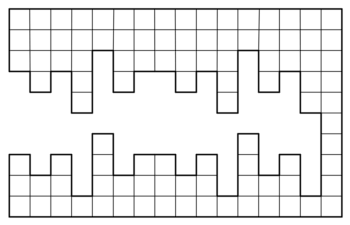
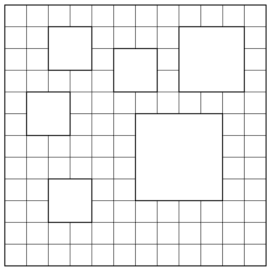
4.

Замените буквы в слове ТРАНСПОРТИРОВКА цифрами (разным буквам соответствуют разные цифры, а одинаковым одинаковые) так, чтобы выполнялось неравенство

Т > Р > А > Н < С < П < О < Р < Т > И > Р > О < В < К < А.

5.

У Пети в кармане несколько монет. Если Петя наугад вытащит из кармана 3 монеты, среди них обязательно найдётся монета «1 рубль». Если Петя наугад вытащит 4 монеты из кармана, среди них обязательно найдётся монета «2 рубля». Петя вытащил из кармана 5 монет. Можете ли вы точно сказать, что это за монеты?

6.

Среди 201 монеты 50 фальшивых. Каждая фальшивая отличается от настоящей по весу на 1 грамм (в ту или в другую сторону). Имеются чашечные весы со стрелкой, показывающей разность масс одной и другой чашки. Вам указали на одну монету. За какое наименьшее число взвешиваний вы заведомо сможете выяснить, фальшивая она или настоящая?

7.

В левом нижнем углу доски 6×8 стоит ладья. Двое игроков по очереди сдвигают ладью либо вверх, либо вправо на произвольное количество клеток. Выигрывает тот, кто поставит ладью в правую верхнюю клетку. Кто из игроков (первый или второй) может действовать так, чтобы выиграть вне зависимости от того, насколько хитёр его противник, и как ему для этого нужно играть?

2-й листок

8.

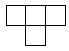
а)

Соберите квадрат 100×100 из четырёхклеточных Т-образных фигурок (таких, как на рисунке справа).

б)

А можно ли собрать квадрат 102×102?

9.

Можно ли расставить охрану вокруг расположенного в степи небольшого секретного объекта так, чтобы ни к объекту, ни к часовым нельзя было незаметно подкрасться? (Каждый часовой стоит неподвижно и видит на 100 м строго вперёд.)