МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 16 (28 февраля 2015 года). Чётность

1.

Можно ли разменять 25 рублей при помощи десяти купюр достоинством в 1, 3 и 5 рублей?

2.

Аня, Катя, Артём и ещё трое их друзей устроили небольшой шахматный турнир. Артём говорит, что в итоге он сыграл 17 партий, Катя — 16, а все остальные — по 11. Можно ли по его словам определить, сколько всего партий было сыграно?

3.

На доске написано в строку 2015 целых чисел. Обязательно ли можно выбрать одно из них так, что после его стирания сумма оставшихся чисел будет чётной?

4.

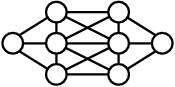
Расставьте в кружочках числа 1, 2, 3, ..., 8 так, чтобы ни в каких двух соединённых отрезком кружочках не оказались бы соседние (то есть отличающиеся на 1) числа.

5.

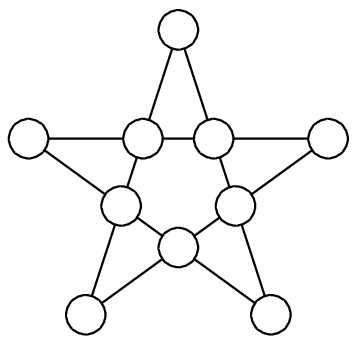
Можно ли в кружочки в пятиконечной звезде расставить 4 единицы, 3 двойки и 3 тройки так, чтобы суммы четырёх чисел, стоящих на каждой из пяти прямых, были одинаковы?

6.

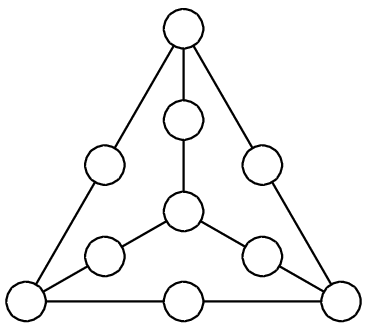
Можно ли в кружочках расставить все цифры от 0 до 9 так, чтобы сумма трех чисел по любому из шести отрезков была бы одной и той же?

7.

Расшифруйте пример на умножение, если буквой Ч зашифрованы чётные цифры (не обязательно одинаковые), а буквой Н — нечётные:

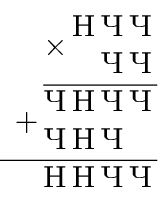
Дополнительные задачи

8.

На доске записано число 123456789. У написанного числа выбираются две соседние цифры, если ни одна из них не равна 0, из каждой цифры вычитается по 1, и выбранные цифры меняются местами (например, из 123456789 можно за одну операцию получить 123436789). Какое наименьшее число может быть получено в результате таких операций?

9.

В ряду из 2009 гирек вес каждой гирьки составляет целое число граммов и не превышает 1 кг. Веса любых двух соседних гирек отличаются ровно на 1 г, а общий вес всех гирь в граммах является чётным числом. Докажите, что гирьки можно разделить на две кучки, суммы весов в которых равны.

10.

Гномы сели за круглый стол и голосованием решили много вопросов. По каждому вопросу можно было голосовать «за», «против» или воздержаться. Если оба соседа какого-либо гнома по какому-нибудь вопросу выбрали один и тот же вариант ответа, то при голосовании по следующему вопросу он выберет этот же вариант. А если они выбрали два разных варианта, то при голосовании по следующему вопросу гном выберет третий вариант. Известно, что по вопросу „Блестит ли золото?” все гномы проголосовали «за», а по вопросу „Страшен ли Дракон?” Торин воздержался. Сколько могло быть гномов?