МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 7 (8 ноября 2014 года)

1.

На лужайке росли 35 жёлтых и белых одуванчиков. После того как 8 белых облетели, а 2 жёлтых побелели, жёлтых одуванчиков стало вдвое больше, чем белых. Сколько белых и сколько жёлтых одуванчиков росло на лужайке вначале?

2.

Артур, Стёпа и Гриша стоят в круг и играют в мяч, пасуя его по часовой стрелке. Вначале мяч был у Артура. У кого он будет после 1001-го паса?

3.

Деревянный куб покрасили снаружи белой краской, каждое его ребро разделили на 4 равные части, после чего куб распилили так, что получились маленькие кубики, у которых ребро в 4 раза меньше, чем у исходного куба.

а)

Сколько получилось маленьких кубиков?

б)

Сколько из них с одной окрашенной гранью?

в)

Сколько из них с двумя окрашенными гранями?

г)

Сколько из них с тремя окрашенными гранями?

д)

Сколько из них неокрашенных?

4.

Незнайка целую неделю вычислял, сколько получится, если перемножить сто двоек. Когда он закончил вычисления и показал результат Шпунтику, тот сразу сказал, что Незнайкин ответ неверен, поскольку оканчивается на 8. А на какую цифру должен оканчиваться правильный ответ?

5.

Вдоль дорожки между домиками Незнайки и Синеглазки росли в ряд цветы: 15 пионов и 15 тюльпанов вперемешку. Отправившись из дома в гости к Незнайке, Синеглазка поливала все цветы подряд. После 10-го тюльпана вода закончилась, и 10 цветов остались не политыми. Назавтра, отправившись из дома в гости к Синеглазке, Незнайка собирал для неё все цветы подряд. Сорвав 6-й тюльпан, он решил, что для букета достаточно. Сколько цветов осталось расти вдоль дорожки?

6.

Незнайка изобрёл два ребуса:

а) АХ + ОХ = УХ; б) ШЕ·СТЬ + 1 = СЕ·МЬ.

Есть ли у них хоть одно решение? (Как обычно, в правильном решении ребуса разные буквы замещают разные цифры, одинаковые — одинаковые.)

7.

Петя и Вася по очереди слева направо пишут цифры 2014-значного числа. Первым ходит Петя. Выясните, кто выигрывает при правильной игре в каждой из следующих ситуаций.

а)

Если в результате получится число, делящееся на 10, выигрывает Вася, иначе — Петя.

б)

Если в результате получится число, делящееся на 7, выигрывает Петя, иначе — Вася.

в)

Если в результате получится число, делящееся на 3, выигрывает Вася, иначе — Петя.

г)

Если в результате получится число, делящееся на 20, выигрывает Вася, иначе — Петя.

д)

Если в результате получится число, делящееся на 13, выигрывает Вася, иначе — Петя.

Задачи на дом

8.

Как из 2013 полосок бумаги шириной 1 и длинами 1, 2, ..., 2013 составить прямоугольник, длина и ширина которого больше 1?

9.

а)

Поросенок Наф-Наф придумал, как сложить брусок из одинаковых кубиков и оклеить его тремя квадратами без щелей и наложений. Сделайте это и вы.

б)

А может ли Наф-Наф добиться, чтобы при этом каждые два квадрата граничили друг с другом?

10.

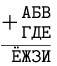Когда Незнайку попросили придумать задачу для математической олимпиады в Солнечном городе, он написал ребус, изображённый на рисунке справа. Можно ли его решить? (Разным буквам должны соответствовать разные цифры.)

11.

На доске написано число 23. Каждую минуту число стирают с доски и на его место записывают произведение его цифр, увеличенное на 12. Какое число окажется на доске через час?