МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 9 (22 ноября 2014 года)

1.

Два мальчика играют на гитарах, а один — на балалайке. Миша с Петей играют на разных инструментах, Петя с Юрой — тоже. На чём играет Миша?

2.

По кругу стоят 12 детей. Мальчики всегда говорят правду мальчикам и врут девочкам, а девочки всегда говорят правду девочкам и врут мальчикам. Каждый из них сказал одну фразу своему соседу справа: «Ты — мальчик» или «Ты — девочка», причём первую из этих фраз сказали ровно 7 детей. Сколько девочек среди собравшихся детей?

3.

Сейчас 16 часов 56 минут. Куда будет показывать минутная стрелка через 100 минут? Через 1000 минут? Через 600000 минут?

4.

Врун всегда лжёт, Рыцарь всегда говорит правду, Хитрец говорит правду или ложь, когда захочет, а Переменчик говорит то правду, то ложь попеременно. Путешественник встретил а) Вруна, Рыцаря и Переменчика; б) Вруна, Хитреца и Переменчика. Все трое встреченных им знают друг друга. Путешественнику же известно, что перед ним указанные трое персонажей, но он не знает, кто из них кто. Сможет ли он, задавая им вопросы, выяснить это?

5.

а)

Как из семи «уголков», каждый из которых склеен из трёх кубиков 1×1×1, и шести отдельных кубиков 1×1×1 составить большой куб 3×3×3?

б)

Можно ли это сделать так, чтобы все отдельные кубики оказались в серединах граней большого куба?

6.

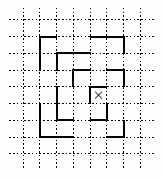
Внутри забора, представляющего собой замкнутую несамопересекающуюся ломаную, заперт тигр. На рисунке видна только часть забора (положение тигра показано крестиком). Нарисуйте, как мог бы выглядеть весь забор (забор может идти только по линиям сетки).

7.

На крыше в ряд сидят 6 котов.
Между Пушком и Мурзиком сидит Кузя и ещё один кот.
Между Рыжиком и Кузей сидит Барсик и ещё один кот.
Между Барсиком и Васькой сидит Пушок и ещё один кот.
Можно ли однозначно определить, как сидят коты, если Васька не крайний и сидит правее Рыжика?

Дополнительная задача

8.

Таня стоит на берегу речки. У неё есть два глиняных кувшина: один — на 5 литров, а про второй Таня помнит лишь то, что он вмещает то ли 3, то ли 4 литра. Помогите Тане определить ёмкость второго кувшина. (Заглядывая в кувшин, нельзя понять, сколько в нём воды.)

Задачи на дом

9.

Можно ли расставить во всех клетках листа клетчатой бумаги 2014×2014 крестики и нолики так, чтобы ни на одной горизонтали, вертикали и диагонали нельзя было встретить три одинаковых знака подряд?

10.

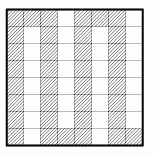
Художник-авангардист Змий Клеточкин покрасил несколько клеток доски размером 8×8, соблюдая правило: каждая следующая закрашиваемая клетка должна соседствовать по стороне с предыдущей закрашенной клеткой, но не должна — ни с одной другой ранее закрашенной клеткой. Ему удалось покрасить 36 клеток. Побейте его рекорд — закрасьте таким образом как можно больше клеток!

11.

Одно трёхзначное число состоит из различных цифр, следующих в порядке возрастания, а в его названии все слова начинаются с одной и той же буквы. Другое трёхзначное число, наоборот, состоит из одинаковых цифр, но в его названии все слова начинаются с разных букв. Какие это числа?