МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 14 (14 февраля 2015 года). Математическая регата

Правила математической регаты

1. В составе каждой команды — 3–5 человек.
2. Соревнование проводится в четыре тура. Каждый тур представляет собой коллективное письменное решение трех задач. Каждая задача оформляется и сдается в жюри на отдельном листе. Каждая команда имеет право сдать только по одному варианту решения каждой из задач.
3. Использование какой-либо математической литературы или калькуляторов запрещено. Мобильные телефоны должны быть отключены.
4. Проверка решений осуществляется жюри после окончания каждого тура.
5. Разбор задач для учащихся осуществляется параллельно с проверкой. Итоги проверки объявляются только после окончания этого разбора. После объявления итогов тура, команды, не согласные с тем, как оценены их решения, имеют право подать заявки на апелляции.
6. Команды-победители и призеры регаты определяются по сумме баллов, набранных каждой командой во всех турах.

Первый тур (10 минут)

1.1 (6 баллов).

Винни-Пух подарил Пятачку и Ослику Иа-Иа по охапке воздушных шариков. Однако у Ослика 6 шариков лопнуло, и он очень огорчился. Тогда Пятачок отдал ему два своих шарика. После этого у Ослика и Пятачка стало по 11 шариков. Сколько шариков Винни-Пух подарил Пятачку, а сколько — Ослику?

1.2 (6 баллов).

В семье 5 детей. Китти на 2 года старше, чем Бетти, но на 2 года младше, чем Данни. Тедди на 3 года старше, чем Анни. Бетти и Анни — близнецы. Кто из детей самый старший?

1.3 (6 баллов).

Расставьте в клетках квадрата 6×6 крестики так, чтобы в каждой строке было ровно два крестика, а в каждом столбце — либо один крестик, либо три крестика.

Второй тур (15 минут)

2.1 (7 баллов).

В ребусе Д + В + А = 11 буквами обозначены три разные ненулевые цифры. Чему может быть равно произведение Д · В · А ? Найдите все варианты и докажите, что других нет.

2.2 (7 баллов).

Друзья Ой-Ой и Эх-Эх — жители Острова Рыцарей и Лжецов. На наши вопросы Ой-Ой ответил: «Мы оба лжецы», а Эх-Эх молча улыбнулся. Определите, кто они на самом деле. Напоминаем, что на Острове Рыцарей и Лжецов живут только рыцари, которые всегда говорят только истинную правду, и лжецы, которые всегда лгут.

2.3 (7 баллов).

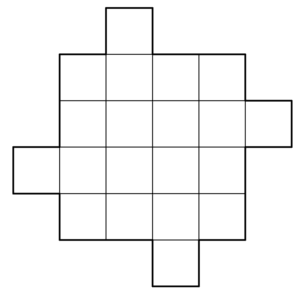
Найдите как можно больше способов разрезать изображённую на рисунке фигурку на четыре равные части. Резать можно только по линиям сетки. Способы, отличающиеся только поворотом доски, считаются одинаковыми.

Третий тур (20 минут)

3.1 (8 баллов).

Собираясь в школу, Миша нашел под подушкой, под диваном, на столе и под столом всё необходимое: тетрадь, шпаргалку, плеер и кроссовки. Под столом он нашел не тетрадь и не плеер. Мишины шпаргалки никогда не валяются на полу. Плеера не оказалось ни на столе, ни под диваном. Что где лежало, если в каждом из мест находился только один предмет?

3.2 (8 баллов).

В надписи РЕГ + АТ + А замените каждую букву на цифру так, чтобы сумма получилась как можно больше. Одинаковые буквы нужно заменять одинаковыми цифрами, а разные — разными. Объяснять, почему ваша сумма наибольшая, не нужно.

3.3 (8 баллов).

Покажите, как разрезать квадрат размером 5×5 клеток на «уголки» шириной в одну клетку так, чтобы все «уголки» состояли из разного количества клеток. Длины «сторон» уголка могут быть как одинаковыми, так и различными.

Четвёртый тур (20 минут)

4.1 (8 баллов).

Некоторые жители Острова Разноцветных Лягушек говорят только правду, а остальные всегда лгут. Трое островитян сказали так:
Бре: На нашем острове нет синих лягушек.
Ке: Бре лгун. Он же сам синяя лягушка!
Кекс: Конечно, Бре лгун. Но он красная лягушка.
Водятся ли на этом острове синие лягушки?

4.2 (8 баллов).

Боря и Миша едут в поезде и считают столбы за окном: «один, два, ...». Боря не выговаривает букву «Р», поэтому при счете он пропускает числа, в названии которых есть буква «Р», а называет сразу следующее число без буквы «Р». Миша не выговаривает букву «Ш», поэтому пропускает числа с буквой «Ш». У Бори последний столб получил номер «сто». Какой номер этот столб получил у Миши?

4.3 (8 баллов).

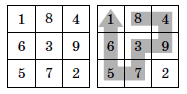
Квадрат 3×3 заполнен цифрами так, как показано на рисунке слева. Разрешается ходить по клеткам этого квадрата, переходя из клетки в соседнюю (по стороне), но ни в какую клетку не разрешается попадать дважды. Петя прошел, как показано на рисунке справа, и выписал по порядку все цифры, встретившиеся по пути, — получилось число 84937561. Нарисуйте другой путь так, чтобы получилось число побольше (чем больше, тем лучше).