
МАЛЫЙ МЕХМАТ МГУ

Кружок 9-10 класса
Руководители Иван Александрович Дорофеев и Степан Львович Кузнецов
2006/2007 учебный год
2006/2007 учебный год
Зимний математический бой
- 1.
- Найдите все такие пары взаимно простых целых положительных чисел a и b, что дробь a/b в десятичной записи имеет вид b,a.
- 2.
- В треугольнике ABC AB = c, AC = b, b > c, AD — биссектриса. Через точку D проведена прямая, перпендикулярная AD и пересекающая AC в точке E. Найдите AE.
- 3.
- Какую максимальную площадь может иметь четырёхугольник, стороны которого последовательно равны 1 − 7a, 7 − 6a, 5 − 3a и 14a + 5? Найдите все значения a, при которых эта максимальная площадь достигается.
- 4.
-
Функция f удовлетворяет уравнению f(x + 1) = f(x) + 2x + 1 (для
всех x). Известно, что f(0) = 0. Чему равно f(2006)?
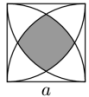
- 5.
- Дан квадрат со стороной a. С центрами в вершинах квадрата построили дуги окружностей радиуса a, заключённые в квадрате. Найдите площадь заштрихованной (см. чертёж) области. (Площадь круга радиуса R равна π R2.)
- 6.
- На шахматной доске 8×8 стоят ладьи — по одной на каждой горизонтали и каждой вертикали. Доску разбили на 4 равных квадрата. Докажите, что число ладей в правом верхнем квадрате равно числу ладей в левом нижнем квадрате.
Вася отметил на плоскости точку симпатическими чернилами и начертил квадрат обычными чернилами. Петя видит квадрат, но не видит точку. Он может начертить прямую и спросить у Васи, по какую сторону от прямой лежит точка. Какое наименьшее число вопросов потребуется задать, чтобы узнать, лежит ли точка внутри квадрата?