МАЛЫЙ МЕХМАТ МГУ

Кружок 9-10 класса

Листок 4. Площади

1.

а)

На стороне AD параллелограмма ABCD взята точка M. Площадь треугольника BMC равна S. Какова площадь параллелограмма?

б)

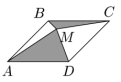Пусть теперь точка M взята внутри параллелограмма и соединена со всеми вершинами (см. рисунок). Площадь заштрихованной части параллелограмма равна S. Найдите площадь параллелограмма.

2.

Докажите, что медианы делят треугольник на 6 равновеликих треугольников.

3.

На сторонах треугольника ABC взяты точки P, Q и R, делящие его стороны в отношениях BP : PC = p, CQ : QA = q, AR : RB = r. Чему равно отношение площадей треугольников PQR и ABC?

4.

Многоугольник периметра P описан около окружности радиуса r. Найдите площадь многоугольника.

5.

Могут ли длины высот треугольника равняться 1, 2 и 3?

6.

Каждая сторона а) треугольника A₁A₂A₃, б) выпуклого четырёхугольника A₁A₂A₃A₄, в) выпуклого n-угольника A₁A₂...A_n продолжена на свою длину так, что точка A_i — середина отрезка A_i-1A'_i, A₁ — середина отрезка A_nA'₁ (в пунктах а) и б) n=3 и n=4 соответственно). Площадь исходного многоугольника равна S. Найдите площадь полученного многоугольника A'₁A'₂...A'_n.

7.

В некоторой стране любые два города соединены либо железной дорогой, либо авиалинией. Докажите, что либо в случае забастовки авиадиспетчеров, либо в случае забастовки машинистов можно будет добраться из каждого города в каждый.

8.

25 жуков сидели по одному в клетках квадратной доски 5×5. Каждый перелетел на соседнюю (по горизонтали или по вертикали) клетку. Докажите, что хотя бы одна клетка освободилась.