МАЛЫЙ МЕХМАТ МГУ

Кружок 9-10 класса

Руководители Иван Александрович Дорофеев и Степан Львович Кузнецов
2006/2007 учебный год

Листок 6. Графы 2

1.: Дан кусок проволоки длиной 120 см. Можно ли, не ломая проволоки, изготовить из него каркас куба с ребром 10 см?
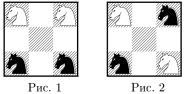
2.: Можно ли, сделав несколько ходов конями из исходного положения (рис. 1), расположить их так, как показано на рис. 2? (Выходить за пределы поля 3×3 не разрешается.)

Определение. Граф называется связным, если для любых двух вершин существует путь, их соединяющий.

Обозначения. Пусть дан связный граф на плоскости (т.е. его вершины суть точки плоскости, а рёбра представлены непересекающимися кривыми, соединяющими вершины). Тогда положим В — число вершин, Р — число рёбер, Г — число частей, на которые рёбра графа разбивают плоскость (граней).

3.: Волейбольная сетка имеет вид прямоугольника размером 50×600 клеток. Какое наибольшее число верёвочек можно перерезать так, чтобы сетка не распалась на куски?
4.: (Формула Эйлера) Докажите, что В − Р + Г = 2.
5.: В квадрате отметили 20 точек и соединили их непересекающимися отрезками друг с другом и с вершинами квадрата так, что квадрат разбился на треугольники. Сколько получилось треугольников?
6.: Докажите, что а) для графа на плоскости 2Р ≥ 3Г, б) для связного графа на плоскости Р ≤ 3В − 6, в) последнее неравенство справедливо для произвольного графа на плоскости.
7.: Докажите, что граф, имеющий пять вершин, каждая из которых соединена ребром с любой другой (полный граф с пятью вершинами), не является плоским (т.е. его нельзя изобразить на плоскости так, чтобы рёбра не пересекались).

Определения. Граф на плоскости называется многоугольным, если каждая его грань есть многоугольник (возможно, с кривыми сторонами). Многоугольный граф называется правильным, если каждая его грань ограничена одним и тем же числом (обозначим его ρ*) рёбер и к каждой вершине сходится одно и то же число (обозначим это число ρ) рёбер.

8.

а): Докажите, что для правильного графа В·(2ρ + 2ρ* − ρρ*) = 4ρ*.
б): Перечислите все правильные графы.
в): Существуют ли правильные многогранники, кроме тетраэдра, куба, октаэдра, додекаэдра и икосаэдра?

Определения. Паросочетанием называется такое подмножество M множества рёбер графа, что из любой вершины исходит не более одного ребра из M.
Вершинным покрытием называется такое подмножество C множества вершин графа, что хотя бы один из концов любого ребра лежит в C.

9.: Докажите, что число рёбер в любом паросочетании не превосходит числа вершин в любом вершинном покрытии.
10*.: (теорема Кёнига – Эгервари) Докажите, что в двудольном графе число рёбер в максимальном (по числу элементов) паросочетании в точности равно числу вершин в минимальном вершинном покрытии.
11.: Приведите пример графа (не двудольного), для которого утверждение теоремы Кёнига – Эгервари не имеет места (то есть число рёбер в любом паросочетании строго меньше числа вершин в любом вершинном покрытии).
12.: (лемма о девушках = лемма Холла) Есть n юношей и n девушек. Каждый юноша знаком с некоторыми девушками. Для любого 0 < k < n + 1 любые k юношей знают не менее k девушек. Назовём множество из k юношей критическим, если они знают ровно k девушек. а) Докажите, что пересечение критических множеств — критическое. б) Докажите, что в этих условиях компанию можно переженить по знакомствам.

Вы видите ошибку? Выделите её и нажмите Ctrl+Enter!