МАЛЫЙ МЕХМАТ МГУ

Кружок 9-10 класса

Руководители Иван Александрович Дорофеев и Степан Львович Кузнецов
2006/2007 учебный год

Листок 16 для 9 класса. Комплексные числа

Теоретические сведения. Комплексными числами называются (формальные) двучлены вида a + bi, a и b — действительные числа, а i — некоторый символ, квадрат которого мы при вычислениях будем отождествлять с числом − 1. Заметим, что при сложении и перемножении таких двучленов опять получается запись того же вида: (a + bi) + (c + di) = (a + c) + (b + d)i, (a + bi)·(c + di) = ac + bci + adi + bdi² = (ac − bd) + (bc + ad)i. Если z = a + bi, то a = Re z называется действительной, а b = Im z — мнимой частью числа z. Для комплексных чисел верны обычные законы сложения и умножения. Число z = a − bi называется сопряжённым к числу z = a + bi.

Замечание В комплексных числах любое квадратное уравнение имеет корень (это следует из формулы для корней). Имеет место более сильное утверждение (основная теорема алгебры): любое уравнение вида P(z) = 0 (P — многочлен) имеет комплексный корень.

1.
Докажите, что z + z и z · z суть действительные числа.
2.
Докажите, что 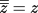, z + w = z + w, zw = z·w.
3.
Вычислите a + bi/c + di.
4.
Вычислите (1 + i)10.
5.
Решите (в комплексных числах) уравнения: а) x² + x + 1 = 0; б) x³ = 1.
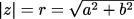Комплексному числу a + bi можно сопоставить точку плоскости с координатами (a,b). Расстояние от этой точки до нуля называется модулем, а φ = arg z — угол между отрезком от 0 до z и осью Ox — аргументом z. Аргумент нуля не определён.
6.
а) Найдите модуль и аргумент следующих комплексных чисел: 1 + i, 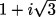. б) Какое комплексное число имеет модуль 5 и аргумент π ⁄ 4? в) Докажите, что если |z| = r, а arg z = φ, то z = r (cos φ + i sin φ) (тригонометрическая форма комплексного числа).
Замечание. Соотношение z = cos φ + i sin φ, где z — комплексное число с модулем 1 и аргументом φ можно считать определением косинуса и синуса: cos φ = Re z, sin φ = Im z.
7.
Докажите, что а) при перемножении комплексных чисел их модули перемножаются, а аргументы складываются; б) (r(cos φ + isin φ))n = rn(cos nφ + i sin nφ) (формула Муавра).
8.
Изобразить на плоскости множество точек, соответствующих комплексным числам, удовлетворяющих неравенству |(z − z1) ⁄ (z − z2)| = λ, где λ > 0 — действительное, а z1 и z2 — комплексные числа.
9.
Будет ли число 2 + i/2 − i в некоторой степени равняться единице?
10.
Сколько существует корней n-й степени из единицы (т.е. таких комплексных чисел ε, что εn = 1)?