МАЛЫЙ МЕХМАТ МГУ

Кружок 9-10 класса

Листок 21. Принцип крайнего

1.

Докажите, что если длины всех сторон треугольника меньше 1, то его площадь меньше 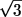/4.

2.

На плоскости даны 2007 точек, никакие три из которых не лежат на одной прямой. Докажите, что найдётся а) треугольник с вершинами в этих точках, не содержащий ни одной из оставшихся точек; б) окружность, проходящая через три из данных точек и не содержащая внутри ни одной из оставшихся точек.

3.

Докажите, что по крайней мере одно из оснований перпендикуляров, опущенных из внутренней точки выпуклого многоугольника на его стороны, лежит на самой стороне (а не на её продолжении).

4.

а)

На шахматной доске стоят несколько ладей. Докажите, что хотя бы одна из них бьёт не более двух других.

б)

На шахматной доске стоят несколько ферзей. Докажите, что какой-то из этих ферзей бьёт не более четырёх других.

в)

Всегда ли верно, что какой-то из ферзей бьёт не более трёх других?

5.

Путешественник выходит из своего родного города и отправляется в самый дальний от него город страны, затем — в город, самый дальний от этого города, и так далее. Расстояния между всеми городами различны. Докажите, что если путешественник не вернулся в родной город после второго перехода, то он никогда в него не вернётся.

6.

Можно ли на плоскости расположить 1000 отрезков так, чтобы каждый отрезок обоими концами упирался строго внутрь других отрезков?

7.

Докажите, что простых чисел бесконечно много.

8.

В парламенте у каждого не более трёх врагов. Докажите, что парламент можно разделить на две палаты так, что у каждого парламентария в своей палате будет не более одного врага.

9.

Имеются два бикфордовых шнура. Шнуры при поджигании горят неравномерно, но каждый полностью сгорает за одну минуту. Как с помощью этих шнуров отмерить а) 30 секунд; б) 45 секунд?