МАЛЫЙ МЕХМАТ МГУ

Кружок 5 класса

Занятие 1 (15.09 и 17.09)

Вступительная олимпиада

1.

В трех ящиках находятся крупа, вермишель и сахар. На первом ящике написано «крупа», на втором – «вермишель», на третьем – «крупа или сахар». Что в каком ящике находится, если содержимое каждого из ящиков не соответствует надписи на нем?

Решение

Решение. Так как каждая надпись не соответствует действительности, то в третьем ящике – вермишель, следовательно, в первом ящике – сахар, а во втором – крупа.

2.

Пять рыбаков съели пять судаков за пять дней. За сколько дней десять рыбаков съедят десять судаков?

Ответ Решение

Ответ. За пять дней.

Решение. Пять рыбаков съели пять судаков за пять дней. Другие пять рыбаков съедят за те же пять дней еще пять судаков. Следовательно, десять рыбаков съедят десять судаков за пять дней.

3.

Сколько всего прабабушек и прадедушек было у всех ваших прабабушек и прадедушек?

Ответ Решение

Ответ. 2⁶ = 64.

Решение. Возможен рисунок в виде «генеалогического дерева» или непосредственный подсчет.

4.

На острове Буяне четыре королевства, причем каждое граничит с тремя остальными. Нарисуйте карту острова так, как вы ее себе представляете.

Ответ

Ответ. Например, cм. рисунок.

5.

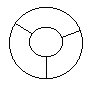
Квадратный торт с четырьмя розочками надо разрезать на 4 равных куска так, чтобы на каждом было по розочке. Нарисуйте, как это сделать.

Ответ

Ответ. см. рисунок.

6.

Найдите частное, если оно в три раза меньше делимого и в восемь раз больше делителя.

Ответ Решение

Ответ. 24.

Решение. Так как частное в три раза меньше делимого, то делитель равен 3. Следовательно, частное равно 24.

7.

Внутри круга отмечена точка, не совпадающая с его центром. Как разрезать круг не более чем на три части, чтобы из этих частей сложить новый круг с центром в отмеченной точке? Можно ли обойтись разрезанием на две части?

Решение

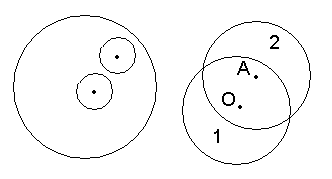
Решение. Один из способов решения: вырезать из данного круга два равных непересекающихся круга так, что центром одного является данная точка А, а центр другого совпадает с центром О данного круга (рис. слева) и поменять их местами.

Разрезанием на две части обойтись можно. Надо провести дугу с центром в точке А того же радиуса, что и у данного круга и отрезанную часть 1 переместить в положение 2 (рис. снизу).

8.

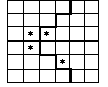
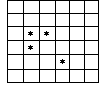
Расставьте на шахматной доске 32 коня так, чтобы каждый бил ровно двух других.

Решение

Решение. Заметим, что если расставить 8 коней в квадрате 3x3 (во все клетки, кроме центральной), то каждый из них будет бить ровно двух других. Теперь разместим 4 таких восьмерки коней по четырём углам доски.