МАЛЫЙ МЕХМАТ МГУ

Кружок 8 класса

Занятие 23 (6 апреля 2013 года).

1.

Коротышки уселись за круглый стол отмечать день рождения Незнайки. Каждый принёс с собой конфеты. Незнайка (тоже, разумеется, сидевший за столом) передал соседу справа блюдо с несколькими конфетами. Сосед взял себе три конфеты, а затем, пересчитав, сколько конфет осталось на блюде, добавил туда ещё столько же своих конфет. После этого он передал блюдо своему соседу справа, тот выбрал себе три конфеты и после этого удвоил оставшееся на блюде число конфет, добавив свои, и далее так поступал каждый коротышка. Наконец, блюдо вернулось к Незнайке. Могло ли случиться, что

а)

сначала Незнайка положил на блюдо 8 конфет, а вернулось к нему блюдо с 7 конфетами?

б)

в начале и в конце путешествия по кругу на блюде было одно и то же число конфет?

2.

Кролик поставил по кругу 12 горшочков с мёдом. Винни-Пух может взять себе любые три подряд стоящие горшочка. Сначала Пух, заглянув в горчшочки №1, №2 и №3, захотел взять именно их, но, посмотрев внимательно, заметил, что стоит чуть-чуть сдвинуться вправо: в горшочках №2, №3, №4 мёда больше. Далее Пух заметил, что взять горшочки №3, №4, №5 ещё более выгодно, и, вдохновлённый результатом, переходил далее и далее, пока не дошёл до тройки №11, №12, №1, которую он и решил взять. Каждый раз очередные три горшочка казались ему более привлекательными по количеству мёда. Докажите, что глазомеру Пуха доверять нельзя.

3.

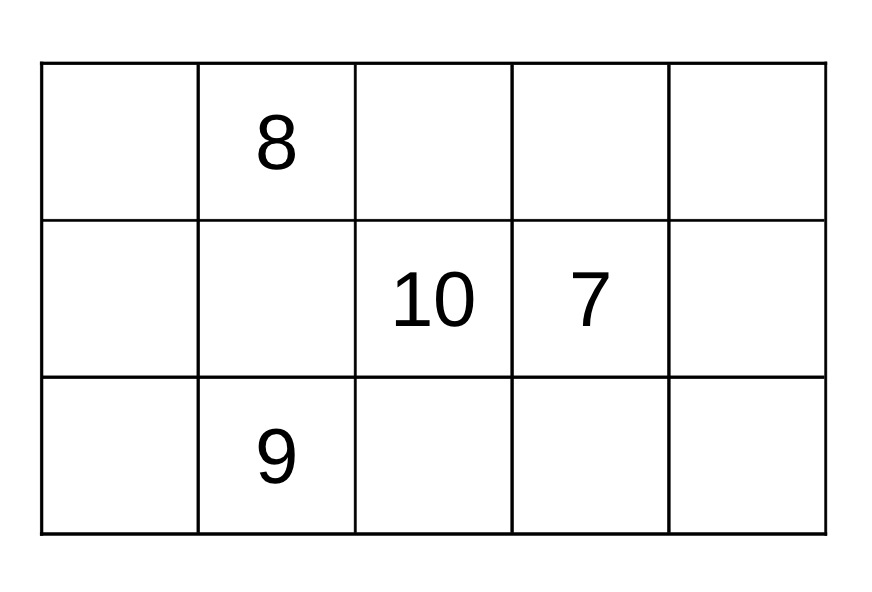
Во всех клетках прямоугольника 3×5 были написаны нули. За одну операцию можно увеличить на 1 все числа в любом квадрате 2×2. Так сделали несколько раз и получили таблицу, некоторые числа в которой известны (см. рисунок). По этим данным выясните, сколько операций было произведено.

4.

На каждой из планет некоторой системы находится астроном, наблюдающий только ближайшую планету. Расстояния между планетами все различны. Незнайка утверждает, что в этой системе 111 планет и все они находятся под наблюдением. Может ли так быть?

5.

Вдоль аллеи стоит 20 столбиков, каждый из которых имеет высоту 1, 2 или 3 метра. Вася, идя в одну сторону, насчитал 13 пар соседних столбиков, в которых высота возрастала. Когда он шёл обратно, то насчитал ровно 5 таких пар. Могло ли так быть?

6.

Внутри выпуклого многоугольника отметили точку. Может ли случиться, что ни один из перпендикуляров, опущенных из этой точки на прямые, содержащие стороны многоугольника, не попадает внутрь стороны?

* * *

7.

По кругу расставлены 100 чисел + 1 и − 1. Для каждого числа подсчитывают произведение 50 чисел, следующих за ним по часовой стрелке. Затем исходные числа стирают, а вместо них записывают вычисленные произведения. Докажите, что после многократного повторения этой операции все числа станут единицами.

8.

У Клары есть комплект всевозможных бус из 4n бусинок, где каждая бусинка либо чёрная, либо белая. Карл испортил один экземпляр, переставив в нем бусинки. Клара хочет перекрасить как можно меньше бусинок в испорченном экземпляре, чтобы снова получились прежние бусы. Какое наибольшее число бусинок ей может понадобиться перекрасить? (Бусы, отличающиеся поворотом или переворотом, считаются одинаковыми.)