МАЛЫЙ МЕХМАТ МГУ

Кружок 8 класса

Занятие 10 (17 ноября 2012 года)

1.

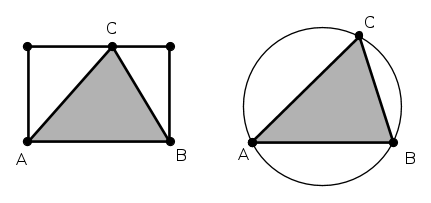
а) При каком положении точки C на границе прямоугольника площадь треугольника ABC будет наибольшей? б) Дана окружность, проходящая через точки A и B. При каком положении точки C на этой окружности площадь треугольника ABC будет наибольшей?

2.

Прямоугольник ABCD площади 1 сложили по прямой так, что точка C совпала с A. Докажите, что площадь получившегося пятиугольника меньше 3/4.

3.

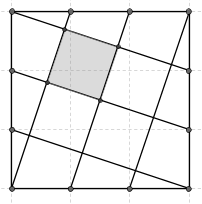
Стороны квадрата длины 3 разбиты на отрезки длины 1 и точки разбиения соединены отрезками, как показано на рисунке. Найдите площадь закрашенной фигурки.

4.

Все целые числа произвольным образом разбиты на две группы. Доказать, что хотя бы в одной из групп найдутся три числа, одно из которых есть среднее арифметическое двух других.

5.

Число a + ¹/_a — целое. Докажите, что число a² + ¹/_a² также целое.

Дополнительные задачи

6.

В обращении есть монеты достоинством в 1, 2, 5, 10, 20, 50 копеек и 1 рубль. Известно, что k монетами можно набрать m копеек. Докажите, что m монетами можно набрать k рублей.

7.

Костя пытался нарисовать на клетчатой бумаге квадрат площади x с вершинами в узлах клеток, а Серёже захотелось нарисовать квадрат площади ¹/_x. Косте удалось нарисовать свой квадрат. Докажите, что и Серёжа сможет исполнить своё желание. (Вершины Серёжиного квадрата не обязаны лежать в узлах клеток. Имеется только один инструмент — линейка, разрешается отмечать точку пересечения двух прямых, отмечать узел cетки и проводить прямую через любые две отмеченные точки.)