МАЛЫЙ МЕХМАТ МГУ

Кружок 8 класса

Занятие 21 (23 марта 2013 года).

1.

По кругу расставлены цифры 1, 2, 3,…, 9 в произвольном порядке. Каждые две цифры, стоящие подряд по часовой стрелке, образуют двузначное число. Чему может быть равна сумма всех девяти таких чисел?

2.

В пять горшочков, стоящих в ряд, Кролик налил три килограмма мёда (не обязательно в каждый и не обязательно поровну). Винни-Пух может одновременно взять только два горшочка, стоящие рядом. Какое наибольшее количество мёда сможет гарантированно взять и съесть Винни-Пух?

3.

Десять детей — пять мальчиков и пять девочек — встали в ряд. Каждый мальчик сказал, сколько детей стоит справа от него, а каждая девочка — сколько детей стоит слева от нее. Докажите, что сумма чисел мальчиков равна сумме чисел девочек.

4.

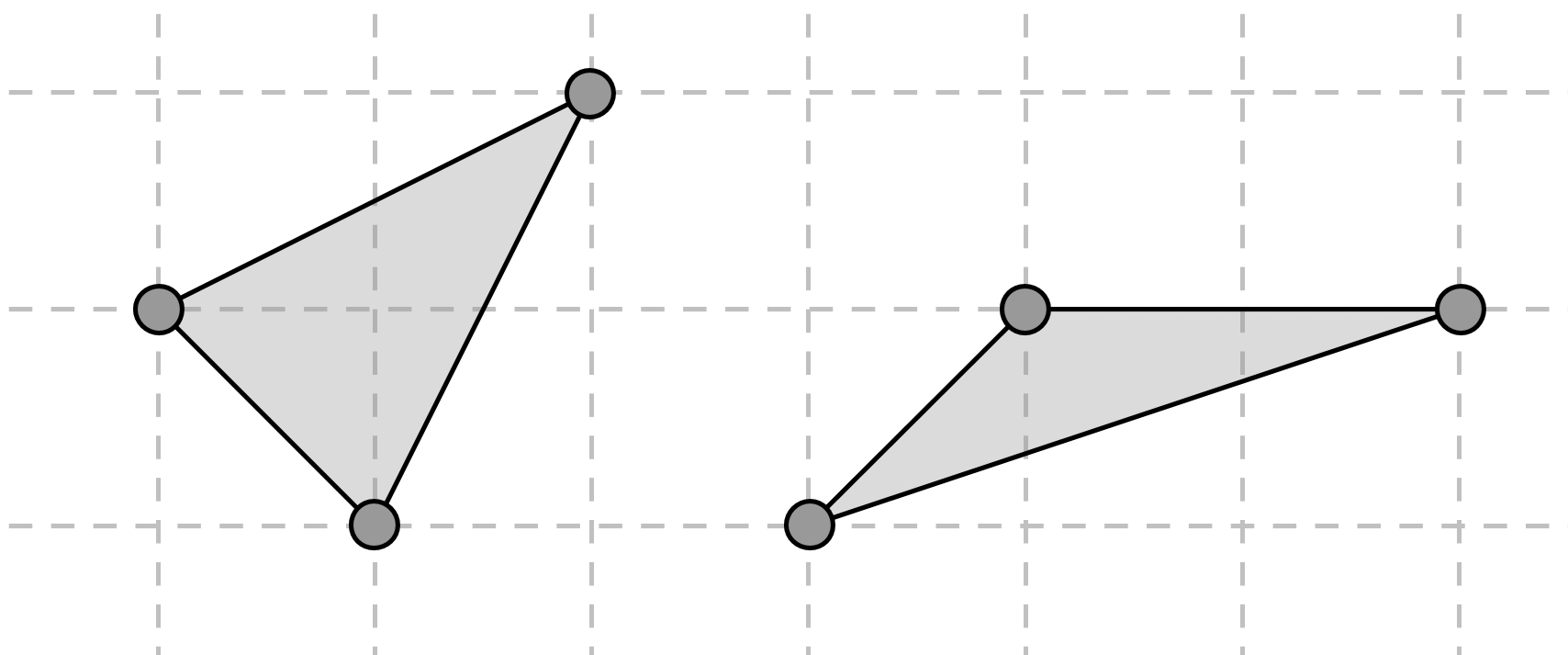
Трое кузнечиков играют в чехарду на клетчатой плоскости. В любой момент любой из кузнечиков может прыгнуть в точку, симметричную его текущему положению относительно точки, где в это время сидит один из двух его друзей. Сейчас кузнечики находятся в вершинах треугольника, изображённого слева. Смогут ли они когда-нибудь оказаться в вершинах треугольника, равного изображённому справа?

5.

Каждый участник чаепития съел на 7 конфет меньше, чем все остальные вместе, но всё же больше одной конфеты. Сколько всего конфет было съедено?

* * *

6.

Какое наибольшее число попарно не бьющих друг друга ладей можно расставить в кубе 8×8×8?

7.

Дети играли в крестики-нолики. Состоялось 5 партий „девочка против девочки” и 12 партий „мальчик против мальчика”. При этом каждый ребенок сыграл партий с девочками на одну меньше, чем партий с мальчиками. Сколько детей играли в крестики-нолики?

8.

Незнайке сообщили два натуральных числа a и b и попросили разбить квадрат на прямоугольники так, чтобы выполнялось следующее свойство: любая вертикальная прямая, пересекающая квадрат, либо содержит сторону какого-то из прямоугольников (или стороны нескольких прямоугольников), либо пересекает ровно a прямоугольников; аналогично, каждая горизонтальная прямая либо пересекает ровно b прямоугольников, либо содержит сторону какого-то прямоугольника. Незнайке хочется, чтобы квадрат был разбит на как можно меньшее число прямоугольников. Помогите Незнайке определить это число (оно может зависеть от a и b).