МАЛЫЙ МЕХМАТ МГУ
Занятие 5. Раскраски
Приведём решения двух задач из прошлого листка.
Сначала разберём задачу 2. Вспомним условие.
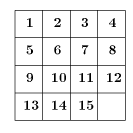Поле для «пятнашек» представляет собой коробочку размером 4×4, в которой находятся 15 фишек (квадратиков 1×1), пронумерованных числами
Первое решение. Будем следить за движением пустого поля внутри коробочки. За один ход оно может сместиться либо вправо, либо влево, либо вверх, либо вниз. Количество ходов вправо должно равняться количеству ходов влево (в противном случае, пустое поле не оказалось бы в том же вертикальном ряду, что и вначале). Значит, общее количество ходов по горизонтали чётно. Аналогично доказывается, что и количество ходов по вертикали тоже чётно. Поэтому, количество всех ходов чётно.
Второе решение. Раскрасим клетки игровой доски в чёрный и белый цвета в шахматном порядке. Тогда при каждом ходе цвет клетки, в которой находится пустое поле меняется. Изначально пустое поле находится в правой нижней клетке, которая окрашена в белый цвет. Значит, после каждого нечётного хода пустое поле находится на чёрной клетке, а после чётного - на белой. В результате оно оказалось на белой клетке, значит всего было сделано чётное число ходов.
Теперь приведём решение задачи 9.
У Васи имеется шахматная доска, из которой вырезали два угловых поля a1 и h8 и 31 кость домино размера в две клетки шахматной доски каждая. Сможет ли Вася покрыть доминошками всю доску?
То, что осталось от шахматной доски, содержит всего 62 клетки и, казалось бы, они могут быть покрыты 31 доминошкой размером в две клетки. Однако ... обе вырезанные клетки чёрные, поэтому из оставшихся клеток 30 чёрных и
Два раза в предыдущих решениях нам помогала шахматная раскраска доски. В случае шахматной доски нам нужно было лишь вспомнить о её существовании, а в случае доски для игры в «пятнашки» пришлось таковую раскраску ввести самим. Часто удачная раскраска (не обязательно шахматная) данного в задаче объекта помогает решить задачу. Задачи, решить которые помогает раскраска, вы найдёте среди предложенных ниже.
| 1. |
Можно ли обойти шахматную доску ходом коня, побывав на каждом поле
по одному разу, начав в левом нижнем углу доски (на поле a1) и
закончив в правом верхнем (на поле h8)? |
| 2. |
|
| 3. | В трапеции ABCD (AB||CD) O — точка пересечения диагоналей. Докажите, что площади треугольников AOD и BOC равны. |
| 4. | Фигура «слонёнок» ходит по шахматной доске, как и слон, по диагонали, но только на одно поле. Можно ли перекрасить клетки шахматной доски (используя чёрный и белый цвета, при этом часть клеток можно оставить покрашенными в свой цвет, а часть — перекрасить на противоположный), чтобы при каждом ходе
«слонёнка» цвет поля менялся? |
| 5. | Какое минимальное количество выстрелов нужно сделать в игре «морской бой», чтобы наверняка «ранить» четырёхпалубный корабль? |
| 6. | В прямоугольную коробочку были сложены несколько прямых тримино (рис. а) так, что они заполняли её целиком (коробочка такова, что лежащие в ней фигурки не могут налегать друг на друга). Затем одно прямое тримино заменили на тримино-уголок (рис. б). Докажите, что образовавшийся набор не поместится в коробочку. |
| 7. | Пространственный лабиринт состоит из 27 кубических комнат, расположенных в виде куба 3×3×3. Из любой комнаты можно перейти в любую соседнюю (через любую стену, пол или потолок). Исследователь лабиринта находится в центральной комнате. Он хочет пройти по всем комнатам, не проходя никакой комнаты дважды. Удастся ли ему это? |
| 8. | Можно ли прямоугольник 11×12 разрезать на Т-тетрамино (рис. в)? |
| 9. | Можно ли число 1999 представить в виде суммы квадратов трёх нечётных чисел? |
| 10. | Разрежьте уголок (рис. б) на четыре равные части. |
Можно ли изображенную на рисунке фигуру из 60 клеток замостить двадцатью прямыми
тримино (размер клетки тримино совпадает с размером
клетки фигуры)?