МАЛЫЙ МЕХМАТ МГУ

Кружок 5 класса

Занятие 9 (20.11.2010). Принцип Дирихле

1.

Восемь кроликов посадили в семь клеток. Докажите, что есть клетка, в которой оказалось по крайней мере два кролика.

Решение

Решение. Если бы ни в какой клетке не было двух кроликов, то всего их было бы не больше, чем клеток, то есть, максимум 7. Но кроликов 8, противоречие.

2.

За победу в математической регате команда из 4 человек получила 10 конфет. Дети поделили конфеты между собой, не разламывая их. Определите, верны ли следующие утверждения:

а)

"кому-то досталось по крайней мере 2 конфеты";

б)

"кому-то досталось по крайней мере 3 конфеты";

в)

"двум людям досталось по крайней мере две конфеты";

г)

"каждому досталась хотя бы одна конфета".

Ответ Решение

Ответ. а) и б) верны, в) и г) нет.

Решение.

а) Если бы никому не досталось две конфеты, то конфет всего было бы не больше 4. Но их 10, противоречие.

б) Если бы никому не досталось три конфеты, то конфет всего было бы не больше 2·4 = 8. Но их 10, противоречие.

в, г) Теоретически, все конфеты мог забрать, например, один человек.

3.

а)

В темной комнате стоит шкаф, в котором лежат 24 чёрных и 24 синих носка. Какое минимальное количество носков нужно взять из шкафа, чтобы из них заведомо можно было составить по крайней мере одну пару носков одного цвета?

б)

Какое минимальное количество носков нужно взять, чтобы заведомо можно было составить хотя бы одну пару носков черного цвета?

в)

Как изменится решение задачи, если в ящике лежат 12 пар чёрных и 12 пар синих ботинок и требуется составить пару одного цвета (как в пункте а) и пару черного цвета (как в пункте б)? Ботинки, в отличие от носков, бывают левыми и правыми.

Ответ Решение

Ответ. а) 3; б) 26; в) 25 и 37.

Решение.

а) Если взять только два носка, то они могут оказаться разных цветов, и составить из них пару не получится. А из трёх носков два точно будут одного цвета.

б) Если взять 25 носков, то 24 из них могут оказаться синими, и составить чёрную пару не получится. Если же взять 26 носков, то синих среди них не может быть больше 24 синих, поэтому точно будут два чёрных.

в) Если взять 24 ботинка, то все они могут оказаться левыми, и составить пару из них не получится. Разобьём мысленно все 48 ботинок на пары. Пар будет 24. Если взять 25 ботинок, то два из них точно будут из одной пары.
Если взять 36 ботинок, то 24 из них могут оказаться синими, а остальные 12 — левыми чёрными, и составить из них чёрную пару не получится. Если взять 37 ботинок, то хотя бы 13 из них будут чёрными, а значит, будет точно хотя бы один чёрный левый и хотя бы один чёрный правый.

4.

В лесу растут миллион ёлок. Известно, что на каждой из них не более 600000 иголок. Докажите, что есть две ёлки с одинаковым количеством иголок.

Решение

Решение. У ёлки может быть 0, 1, 2, ..., 600000 иголок. 600001 возможный вариант, а ёлок больше (1000000). Значит, какой-то вариант точно повторяется, т.е. найдутся две ёлки с одинаковым количеством иголок.

5.

В школе 30 классов и 1000 учащихся. Докажите, что есть класс, в котором не менее 34 учеников.

Решение

Решение. Если такого класса нет, то учеников в школе не может быть больше, чем 33·30 = 990 < 1000, противоречие.

6.

В квадратном ковре со стороной 4 метра моль проела 15 дырок. Докажите, что из этого ковра можно вырезать коврик со стороной 1 метр, в котором дырок не будет.

Решение

Решение. Разобьём ковёр на 16 маленьких ковриков размером 1×1. Так как дырок всего 15, хотя бы один квадратик окажется без дырок. Его и можно вырезать.

7.

В финальном матче школьного чемпионата по баскетболу команда 5А забила 9 мячей. Докажите, что найдутся два игрока этой команды, забившие поровну мячей. (В команде по баскетболу 5 игроков.)

Решение

Решение. Предположим, что такие два игрока не найдутся. Тогда все пять игроков забили разное количество мячей. Пусть первый игрок ничего не забил, второй забил один мяч, третий — два, четвёртый — три, пятый — четыре. Тогда всего игроки забили 10 мячей. Если же кто-то забил больше, чем мы предположили, то и всего мячей было забито больше. Но поскольку по условию игроки забили 9 мячей, наше предположение неверно. Значит, есть два игрока, забившие поровну.

8.

Верно ли, что в вашей аудитории есть по крайне мере два человека, имеющие одинаковое число друзей в этой аудитории? Верно ли это для любой аудитории Малого мехмата?

Решение

Решение. Да, верно. Проведём рассуждения сразу для любой аудитории.
Пусть в аудитории n человек, и у всех из них разное количество друзей. Друзей может быть 0, 1, 2, ..., (n − 1). Всего n возможных вариантов. А так как человек тоже n, то все эти варианты используются. Значит, есть человек, у которого 0 друзей, т. е. который ни с кем не дружит. И есть человек, у которого (n − 1) друг, т.е. который дружит со всеми. Однако этого быть не может, т.к. эти два человека должны одновременно и дружить, и не дружить друг с другом. Получаем противоречие. Значит, два человека с одинаковым количеством друзей всегда найдутся.

Дополнительные задачи

9.

Каждая клетка таблицы 2011×2011 покрашена в один из 2010 цветов. За ход можно взять строку или столбец и, если там есть две клетки одного цвета, перекрасить эту строку или столбец в этот цвет. Всегда ли можно за несколько ходов покрасить всю таблицу в один цвет?

Ответ Решение

Ответ. Всегда.

Решение. Возьмём любую строку. Так как цветов 2010, а клеток в строке — 2011, есть по крайней мере две клетки одного цвета. Значит, мы можем перекрасить всю строку в этот цвет. Воспользуемся этим и покрасим каждую строку в какой-нибудь цвет. Теперь у нас есть 2011 строк, покрашенные в 2010 цветов. Значит, по крайней мере две строки покрашены в один цвет (допустим, красный). То есть, в любом столбце есть две красные клетки. Покрасим все столбцы в красный цвет — все клетки доски будут покрашены в один цвет.

10.

Можно ли клетки доски 5×5 покрасить в четыре цвета так, чтобы клетки, стоящие на пересечении любых двух строк и любых двух столбцов, были покрашены не менее, чем в три цвета?

Решение

Решение. Нельзя.
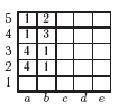
Предположим, что существует раскраска таблицы 5×5, удовлетворяющая условию. Рассмотрим эту таблицу.

В каждом столбце найдется цвет, в который покрашены по крайней мере две клетки этого столбца. Назовем такой цвет преобладающим для данного столбца (возможно, у какого-то столбца будет два преобладающих цвета). Аналогично, какой то цвет (назовем его 1) будет преобладающим для двух столбцов. Поскольку от перестановки строк и столбцов ничего не зависит, будем считать, что это столбцы a и b. Также можем считать, что в первом столбце цветом 1 покрашены клетки a4 и a5. Тогда клетки b4 и b5 должны быть покрашены какими-то двумя различными цветами, отличными от цвета 1. Пусть они покрашены цветами 2 и 3, а поскольку цвет 1 — преобладающий для столбца b, можем считать, что клетки b2 и b3 покрашены цветом 1. Рассмотрим клетку a3. Выбрав 3 и 4 строку и столбцы a и b, мы получим, что клетка a3 не может быть покрашенной цветами 1 и 3. Выбрав 3 и 5 строку и столбцы a и b, мы получим, что клетка a3 не может быть покрашенной цветами 1 и 2. То есть клетка a3 покрашена цветом 4. Но из аналогичных рассуждений мы получаем, что и клетка a2 покрашена цветом 4. То есть квадрат, состоящий из клеток a3, a2, b3 и b2, покрашен в два цвета — противоречие.