МАЛЫЙ МЕХМАТ МГУ

Кружок 5 класса

Занятие 24 (23.04.2011). Геометрические конструкции

1.

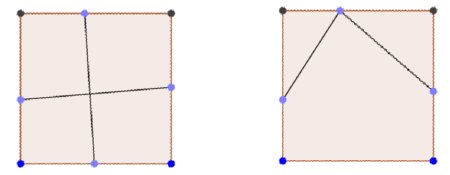
У двух человек было два квадратных торта. Каждый сделал на своём торте по два прямолинейных разреза от края до края. При этом у одного получилось три куска, а у другого — четыре. Могло ли такое быть?

Ответ Решение

Ответ. Да, могло.

Решение.

2.

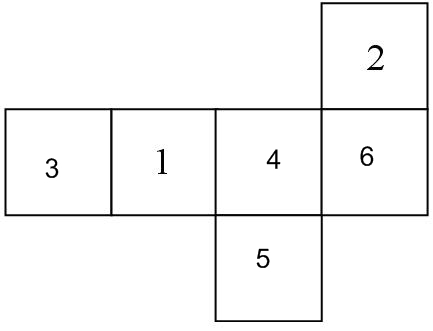
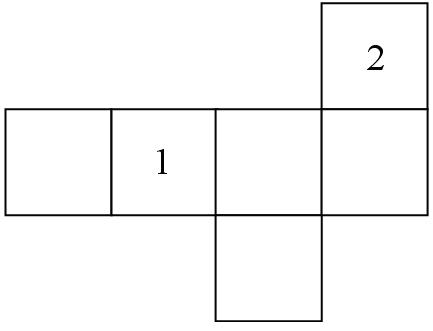
На рисунке изображена развертка кубика. На ней проставлены только числа: 1 и 2. Расставьте остальные числа: 3, 4, 5, 6 — так, чтобы сумма чисел на любых двух противоположных гранях была равна 7.

Решение

Решение.

3.

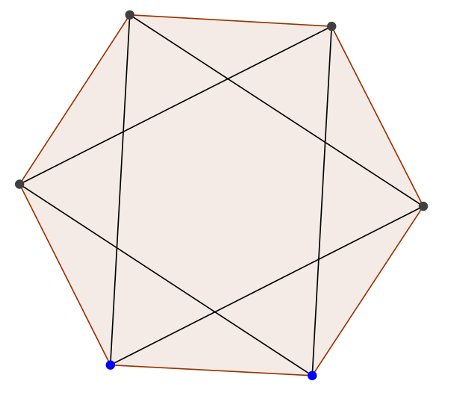
Можно ли на плоскости отметить 6 точек и соединить их отрезками так, чтобы каждая была соединена ровно с четырьмя другими?

Ответ Решение

Ответ. Да, можно.

Решение.

4.

Верно ли, что среди любых пяти отрезков найдутся три, из которых можно составить треугольник?

Ответ Решение

Ответ. Нет, не верно.

Решение. Пусть отрезки имеют длины 1, 2, 4, 8, 16. Нетрудно видеть, что для любых трех отрезков a < b < c верно, что a + b < c. Значит, треугольник составить не удастся.

5.

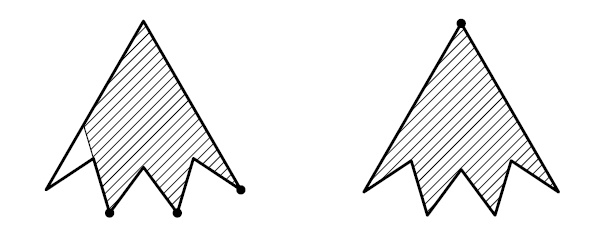
Кролик, готовясь к приходу гостей, повесил в трёх углах своей многоугольной норы по лампочке. Пришедшие к нему Винни-Пух и Пятачок увидели, что не все горшочки с мёдом освещены. Когда они полезли за мёдом, две лампочки разбились. Кролик перевесил оставшуюся лампочку в некоторый угол так, что вся нора оказалась освещена. Могло ли такое быть?

Ответ Решение

Ответ. Да, могло

Решение. Пример см. на рис. Лампочки обозначены кружочками.

6.

Поставьте на плоскости 9 точек так, чтобы никакие 4 не лежали на одной прямой, но из любых шести нашлись 3, лежащие на одной прямой. (На рисунке проведите все прямые, на которых лежат по три отмеченные точки.)

Решение

Решение.

Далее несложным перебором легко показать, что данная конфигурация удовлетворяет условию.

7.

Каждую грань куба разбили на четыре одинаковых квадрата. Можно ли каждый из получившихся квадратов покрасить в один из трёх цветов так, чтобы любые два квадрата, имеющие общую сторону, были покрашены в разные цвета?

Ответ Решение

Ответ. Да, можно.

Решение.

8.

На клетчатой бумаге отмечен прямоугольник размером 2×6. Можно ли раскрасить узлы клеток, лежащие на границе и внутри этого прямоугольника (всего их 21), в два цвета так, чтобы никакие четыре одноцветных узла не оказались в вершинах прямоугольника со сторонами, идущими вдоль линий сетки?

Ответ Решение

Ответ. Нет, нельзя.

Решение. Разобьем прямоугольник из условия на 7 троек из 3 точек. Заметим, что если какие-то две тройки совпадают, то найдется искомый прямоугольник, т.к. в каждой тройке одного из двух цветов хотя бы 2 точки. Всего таких комбинаций 2·2·2 = 8. Осталось заметить, что если выбрана комбинация из трех точек цвета 1, то не выбраны еще хотя бы 3 тройки (в каждой из них ровно две точки цвета 1). Таким образом, найдутся две одинаковые тройки.