МАЛЫЙ МЕХМАТ МГУ

Кружок 5 класса

Занятие 14 (12.02.2011). Можно или нельзя

1.

Ваня говорит: „Позавчера мне было ещё только 10 лет, а в следующем году исполнится уже 13”. Может ли такое быть?

Ответ Решение

Ответ. Да, может.

Решение. Пусть Ваня родился 31 декабря 1999 года. А сегодня 1 января 2011 года. Тогда позавчера, 30 декабря, Ване было 10 лет. На следующий день, 31 декабря, будет его День Рождения, и ему исполнится 11 лет. В этом, 2011 году ему исполнится 12 лет, а в следующем, 2012 году ему исполнится 13 лет.

2.

Можно ли на шахматной доске расставить 9 ладей так, чтобы они не били друг друга?

Ответ Решение

Ответ. Нет, нельзя.

Решение. В каждом столбце шахматной доски может стоять не более одной ладьи. Значит, на всей доске может стоять не более 8 ладей. Но 9 > 8, значит, так расставить 9 ладей не удастся.

3.

а)

Существуют ли такие два последовательных натуральных числа, что сумма цифр каждого из них делится на 4?

Ответ Решение

Ответ. Да, существуют.

Решение. Например, 39 и 40.

б)

А два последовательных числа с равной суммой цифр?

Ответ Решение

Ответ. Нет, не существуют.

Решение. Известно, что число дает такой же остаток при делении на 3, что и сумма его цифр. У двух последовательных чисел остатки при делении на 3 разные, значит, и у сумм их цифр тоже разные. Таким образом, они не могут быть равны.

4. Может ли в месяце быть

а)

3 воскресенья;

Ответ Решение

Ответ. Нет, не может.

Решение. Предположим, что это произошло, например, в месяц M. Ясно, что если бы M начинался в понедельник, то воскресений в нем было не больше, чем есть сейчас. Но тогда бы в M было всего три недели и еще 6 дней, т.е. всего 27 дней. Но минимальное количество дней в месяце — 28. Значит, такого не может быть.

б)

4 воскресенья;

Ответ Решение

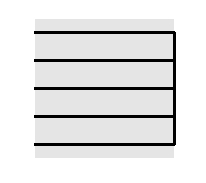
Ответ. Да, может.

Решение. См. пример на рисунке. Это февраль 2011 года.

	1	2	3	4	5	6
7	8	9	10	11	12	13
14	15	16	17	18	19	20
21	22	23	24	25	26	27
28

в)

5 воскресений;

Ответ Решение

Ответ. Да, может.

Решение. См. пример на рисунке. А это май 2011 года.

						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28	29
30	31

г)

6 воскресений?

Ответ Решение

Ответ. Нет, не может.

Решение. Если такое возможно, то в этом месяце умещается целиком 5 недель. Т.е. в нем хотя бы 35 дней. Но такого быть не может.

5.

Можно ли разрезать квадрат на квадратики двух размеров так, чтобы маленьких было столько же, сколько и больших?

Ответ Решение

Ответ. Да, можно.

Решение.

6.

Кролик, готовясь к приходу гостей, повесил в трёх углах своей многоугольной норы по лампочке. Пришедшие к нему Винни-Пух и Пятачок увидели, что не все горшочки с мёдом освещены. Когда они полезли за мёдом, две лампочки разбились. Кролик перевесил оставшуюся лампочку в некоторый угол так, что вся нора оказалась освещена. Могло ли такое быть?

Ответ Решение

Ответ. Да, могло.

Решение. Пример см. на рис. Лампочки обозначены кружочками.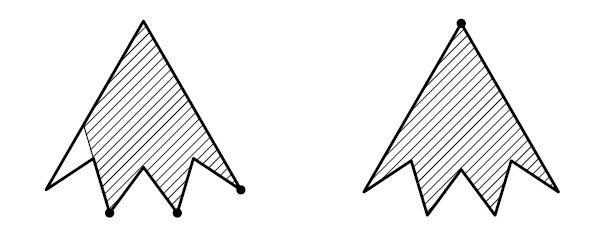

7.

Лиса и два медвежонка делят 100 конфет. Лиса раскладывает конфеты на три кучки; кому какая достанется — определяет жребий. Лиса знает, что если медвежатам достанется разное количество конфет, то они попросят её уравнять их кучки, и тогда она заберёт излишек себе. После этого все едят доставшиеся им конфеты.

а)

Придумайте, как Лисе разложить конфеты по кучкам так, чтобы съесть ровно 80 конфет (ни больше, ни меньше).

Ответ Решение

Ответ. 10, 10 и 80 конфет.

Решение. Покажем, что ответ удовлетворяет условию. Если Лисе достанется 80 конфет, то задача решена. Если ей достанется 10 конфет, то ей придется уровнять кучки медвежат и забрать 70 конфет. Так, она съесть 10 + 70 = 80 конфет.

б)

Может ли Лиса сделать так, чтобы в итоге съесть ровно 65 конфет?

Ответ Решение

Ответ. Нет, не может.

Решение. Медвежата съедят одинаковое число конфет. Значит, в сумме они съедят четное число конфет. Но т.к. 100 — четное число, то и Лиса съест четное число. Но 65 — нечетное, т.е. такого не может быть.

8.

На территории страны, имеющей форму квадрата со стороной 1000 км, находится 51 город. Страна располагает средствами для прокладки 11000 км. Сможет ли правительство страны соединить сетью дорог все свои города?

Ответ Решение

Ответ. Да, сможет.

Решение. Построим 5 горизонтальных дорог длиной 1000 км так, чтобы верхняя и нижняя отставали от верхней и нижней границы на 100 км, а между соседними дорогами было расстояние 200 км (см. рис.). Еще построим вертикальную дорогу, соединяющую верхнюю и нижнюю. Уже построено 5·1000 + 800 = 5800 км дорог. Заметим, что дороги образуют сеть. То есть чтобы все города образовывали сеть, достаточно соединить каждый из них с уже построенными дорогами. Заметим, что расстояние от любого города до ближайшей горизонтальной дороги не превосходит 100 км. Значит, сумма таких расстояний не превосходит 51·100 = 5100 км. 5100 + 5800 < 11000, значит, стране удастся справится.