МАЛЫЙ МЕХМАТ МГУ

Кружок 5 класса

Занятие 7 (06.11.2010). Математическая регата

1 тур (10 минут)

1.

У скольких трёхзначных чисел средней цифрой является 0?

Решение Ответ

Решение. Подходят числа:
100, 101, 102, ..., 109;
200, 201, 202, ..., 209;
.....................
900, 901, 902, ..., 909.
Всего 9 рядов по 10 чисел. Значит, таких чисел 10·9 = 90.

Ответ. 90.

2.

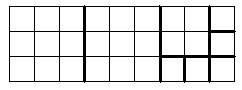
Разрежьте прямоугольник 3×9 на восемь квадратов.

Решение

Решение.

3.

У 28 человек класса на собрание пришли папы и мамы. Мам было 24, пап — 18. У скольких учеников на собрание пришли одновременно и папа, и мама?

Решение Ответ

Решение. Если бы у каждого ученика на собрание пришёл только кто-то один из родителей, то всего родителей было 28. Но их 24 + 18 = 42. „Превышение” получилось из-за того, что у некоторых детей пришли и мама, и папа. Это „превышение” равно 42 − 28 = 14. Значит, и мама, и папа пришли у 14 учеников.

Ответ. 14.

2 тур (15 минут)

1.

Восемь кустов малины растут в ряд, причём количество ягод на любых двух соседних кустах отличается на 1. Может ли всего быть 2011 ягод?

Решение

Решение. Не может.
На любых двух соседних кустах количества ягод отличаются на один, а значит, имеют разную чётность. Тогда эти количества чередуются. Т.е. на первом кусте нечётное число ягод, на втором — чётное, на третьем — нечётное и т.д. Или наоборот, на первом кусте — чётное, на втором — нечётное, на третьем — чётное и т.д. В любом случае, ровно на четырёх кустах будет нечётное число ягод, а значит, общее количество чётно, и 2011 быть равно не может.

2.

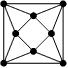
Нарисуйте восемь точек и соедините их отрезками так, чтобы отрезки не пересекались и каждая точка была бы вершиной ровно четырёх отрезков.

Решение

Решение.

3.

У директора Малого мехмата спросили: „Сколько команд будет участвовать в математической регате?”. Он сказал: „Меньше тридцати двух”. Потом подумал и сказал: „Нет, меньше тридцати одной”, а, подумав ещё минуту, добавил: „Наверное, всё-таки меньше тридцати трёх”. Сколько команд участвовало в регате, если верными оказались ровно два из этих утверждений?

Решение Ответ

Решение. Из верности второго утверждения следует верность остальных двух. Значит, оно неверно, а первое и третье верны. Получается, что команд было точно хотя бы 31, но меньше 32. Значит, участвовала 31 команда.

Ответ. 31.

3 тур (15 минут)

1.

Вычислите сумму 11 + 12 + … + 70.

Решение Ответ

Решение. Разобьём числа на пары: первое с последним (11 − 70), второе с предпоследним (2 − 69) и т.д. Получится (70 − 10):2 = 30 пар, в каждой из которых сумма чисел равна 81. Тогда исходное выражение равно 81·30 = 2430.

Ответ. 2430.

2.

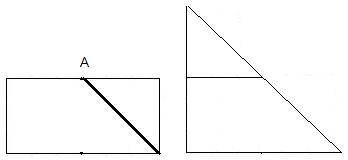
Разрежьте прямоугольник прямолинейным разрезом на две части, из которых можно сложить треугольник.

Решение

Решение.

3.

В городе Глупове каждый житель — полицейский, вор или обыватель. Полицейские всегда врут обывателям, воры — полицейским, обыватели — ворам, а во всех остальных случаях жители Глупова говорят правду. Однажды, когда несколько глуповцев водили хоровод, каждый сказал своему правому соседу: „Я — полицейский”. Сколько в этом хороводе было обывателей?

Решение Ответ

Решение. Заметим, что правый сосед вора, которому этот вор врет, — обязательно полицейский, а правый сосед полицейского, которому этот полицейский говорит правду, — вор или полицейский. Получается, что если в хороводе есть хотя бы один вор или полицейский, то обывателей в этом хороводе нет. Из одних обывателей хоровод тоже состоять не может, так как тогда они лгали бы друг другу. Значит, обывателей в хороводе не было.

Ответ. 0.

4 тур (20 минут)

1.

В примере на сложение цифры заменили звёздочками. Получилось ** + *** = ****. Известно, что каждое из слагаемых и сумма не изменятся, если прочитать их справа налево. Восстановите исходный пример.

Решение Ответ

Решение. Первые два числа не могут быть больше 99 и 999 соответственно. Значит, их сумма, равная третьему числу, не превосходит 99 + 999 = 1098 < 2000. Тогда у третьего числа первая цифра (а значит, и последняя) равна 1: ** + *** = 1**1.
Если у второго числа первая цифра меньше 9, то его значение не превосходит 898. Тогда сумма первого и второго числа не превосходит 99 + 898 = 997 < 1000. Такого быть не может, так как третье число четырёхзначное. Тогда у второго числа первая (а значит, и последняя) цифра должна быть равна 9: ** + 9*9 = 1**1.
Чтобы при сложении 9 на конце получалось 1, последняя (а значит, и первая) цифра первого числа должна быть равна 2: 22 + 9*9 = 1**1.
У второго числа оставшаяся неизвестная цифра должна быть больше 6, так как иначе сумма не будет четырёхзначной: 22 + 969 = 991 < 1000. Значит, она равна 7, 8 или 9. Разберём эти три варианта:
22 + 979 = 1001;
22 + 989 = 1011;
22 + 999 = 1021.
Подходит только первый вариант.

Ответ. 22 + 979 = 1001.

2.

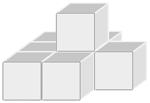
Как поставить на стол 8 одинаковых кубиков так, чтобы со всех сторон полностью были видны ровно 23 грани кубиков, а остальные грани видны не были?

Решение

Решение.

3.

Семья ночью подошла к мосту. Папа может перейти его за 1 минуту, мама — за 2, малыш — за 5, а бабушка — за 10 минут. У них есть один фонарик. Мост выдерживает только двоих. Как им перейти мост за 17 минут? (Если переходят двое, то они идут с меньшей скоростью. Двигаться по мосту без фонарика нельзя. Светить издали нельзя. Носить друг друга на руках нельзя. Кидаться фонариком тоже нельзя.)

Решение

Решение. Переходят папа с мамой (2), папа возвращается (1), переходят малыш с бабушкой (10), мама возвращается (2), и папа с мамой переходят (2). 2 + 1 + 10 + 2 + 2 = 17.