МАЛЫЙ МЕХМАТ МГУ

Кружок 5 класса

Занятие 20 (26.03.2011). Разные задачи

1.

У Кости есть 10 палочек длиной 50 см. Он хочет распилить их так, чтобы получилось 50 палочек длиной 10 см. Сколько распилов ему придется сделать?

Ответ Решение

Ответ. 40.

Решение. Для этого нужно каждую палочку разделить на 5 частей по 10 см. Т.е. на каждой палочке сделать 4 распила. Тогда всего распилов будет 4·10=40.

2.

Денежной единицей Украины является гривна. Можно ли с помощью десяти купюр номиналом в 1 и 5 гривен отсчитать сумму в 31 гривну?

Ответ Решение

Ответ. Нет, нельзя.

Решение. 1 и 5 — нечетные числа. Сумма десяти нечетных чисел четна. Значит, 31 гривну отсчитать не удастся.

3.

В квадрате 7×7 закрасьте несколько клеток так, чтобы в каждой строке и в каждом столбце было ровно три закрашенные клетки.

Решение

Решение.

4.

У скольких трехзначных чисел средней цифрой является 0?

Ответ Решение

Ответ. У 90.

Решение. Первой цифрой может быть любая от 1 до 9 (всего 9), а последней — любая от 0 до 9 (всего 10). Значит, таких чисел 9·10=90.

5.

На острове рыцарей и лжецов (рыцари всегда говорят правду, а лжецы всегда лгут) в некоторой компании каждый заявил остальным: «Среди вас — два рыцаря». Сколько рыцарей могло быть в этой компании?

Ответ Решение

Ответ. 3 или 0.

Решение. Предположим, что был хотя бы один рыцарь. Тогда, кроме него, должно быть еще ровно два рыцаря. Всего будет три рыцаря. Ясно, что компания, в которой ровно 3 рыцаря и любое количество лжецов удовлетворяет условию.
Пусть не было рыцарей. Нетрудно видеть, что компания из одних лжецов также удовлетворяет условию.

6.

В магазине продается шоколад в виде букв английского алфавита. Одинаковые буквы имеют одинаковую цену, а разные — разную. Известно, что слово ONE стоит $6, слово TWO стоит $9, а слово ELEVEN стоит $16. Сколько стоит слово TWELVE?

Ответ Решение

Ответ. $19.

Решение. Возьмем два слова ELEVEN и TWO. Заберем из этих букв одну букву O, одну N и одну E. Тогда из оставшихся букв можно сложить слово TWELVE. Значит, оно стоит 16 + 9 − 6 = 19 долларов.

7.

Сеня взял в долг у Гоши 19 рублей, обязуясь вернуть их в течение 4 месяцев. Причем каждый месяц сумма выплаты должна расти, составлять целое число рублей и нацело делиться на сумму выплаты в предыдущем месяце. Какую сумму выплатит Сеня в последний месяц?

Ответ Решение

Ответ. 12 рублей.

Решение. Заметим, что если в текущем месяце Сеня выплатил x рублей, то в следующем месяце Сеня выплатит хотя бы 2x рублей. Таким образом, если в первый месяц Сеня выплатил x рублей, то всего он выплатит не менее x + 2x + 4x + 8x = 15x рублей. Т.к. 15x ≤ 19, то x = 1. Пусть во втором месяце Сеня выплатил y рублей. Тогда всего он выплатит не менее 1 + y + 2y + 4y = 1 + 7y рублей. 7y + 1 ≤ 19 и y > 1, значит, y = 2. Если в третьем месяце Сеня выплатит не менее 6 рублей, то в последнем не меньше 12, но 12 + 6 + 2 + 1 = 21 > 19. Значит, в третьем месяце Сеня выплатил 4 рубля. Тогда в последний месяц Сеня выплатил 19 − 1 − 2 − 4 = 12 рублей.

8.

Найдите наибольшее натуральное число, любые две последовательные цифры которого образуют точный квадрат.

Ответ Решение

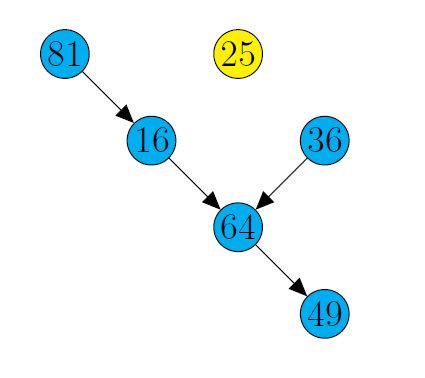
Ответ. 81649.

Решение. Заметим, что в этом числе нет нулей, т.к. нет точного квадрата из двух цифр, оканчивающегося на ноль. Тогда оставшихся возможных вариантов соседних цифр, образующих квадрат, всего 6: 16, 25, 36, 49, 64, 81. Будем соединять числа ab и bc стрелкой, если после ab можно дописать c, не нарушив условие задачи, т.е. bc — точный квадрат. Тогда любой путь по стрелкам — число, удовлетворяющее условию задачи. Длина максимального пути — 3, причем такой путь один. Пройдя по этому пути, получим наибольшее число — 81649.