МАЛЫЙ МЕХМАТ МГУ

Занятие 16. РАСКРАСКИ
| 1. | а) Разрежьте шахматную доску на доминошки размером 1×2. б) Разрежьте шахматную доску без левой нижней и левой верхней угловых клеток на доминошки 1×2. в) Можно ли разрезать шахматную доску без левой нижней и правой верхней угловых клеток на доминошки 1×2? | |||||||||||||||||||||||||||||||||||
| 2. | Замок имеет форму прямоугольника 5×7 клеток. Каждая клетка кроме центральной — комната. А в центральной — бассейн. В каждой стене (стороне клетки), разделяющей две соседние комнаты, есть дверь. Можно ли, не выходя из замка и не заходя в бассейн, обойти все комнаты, побывав в каждой ровно по одному разу? | |||||||||||||||||||||||||||||||||||
| 3. | Можно ли прямоугольную доску размером 5×9 разрезать на уголки | |||||||||||||||||||||||||||||||||||
| 4. | Можно ли доску размером 8×8 с вырезанной правой верхней клеткой разрезать на триминошки | |||||||||||||||||||||||||||||||||||
| 5. | Можно ли шахматную доску разрезать на | |||||||||||||||||||||||||||||||||||
| 6. | Можно ли доску размером 10×10 покрыть фигурами вида | |||||||||||||||||||||||||||||||||||
| 7. | На доске 8×8 для «морского боя» стоит трёхпалубный корабль (прямоугольник 1×3). Какого наименьшее число выстрелов достаточно, чтобы наверняка ранить его? | |||||||||||||||||||||||||||||||||||
| 8. | Прямоугольное дно коробки было выложено квадратами 2×2 и прямоугольниками 1×4. Один квадрат потеряли и вместо него нашли прямоугольник. Можно ли теперь сложить дно этой коробки? | |||||||||||||||||||||||||||||||||||
| 9. | Из листа клетчатой бумаги размером 29×29 вырезали 99 квадратиков размером 2×2. Докажите, что можно вырезать ещё хотя бы один такой квадратик. Домашние задачи | |||||||||||||||||||||||||||||||||||
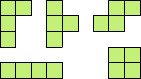
| 10. | Можно ли из пяти изображённых фигур сложить прямоугольник 4×5?
| |||||||||||||||||||||||||||||||||||
| 11. | На каждой клетке доски 9×9 сидит по одному жуку. В некоторый момент времени жуки взлетели и приземлились. | |||||||||||||||||||||||||||||||||||
| 12. | Пете подарили набор «Юный паркетчик», состоящий из 12 триминошек Дополнительные задачи | |||||||||||||||||||||||||||||||||||
| 13. | Замок имеет форму правильного треугольника, разделённого на 25 маленьких залов той же формы. В каждой стене между залами проделана дверь. Путник ходит по замку, не посещая более одного раза ни один из залов. Найдите наибольшее число
залов, которое ему удастся посетить. | |||||||||||||||||||||||||||||||||||
| 14. | Дан куб 6×6×6. Найдите максимальное число параллелепипедов 4×1×1, которые можно поместить в этот куб без пересечений. | |||||||||||||||||||||||||||||||||||
| 15. | В квадратный замок 8×8, разбитый на квадратные комнаты, зашёл маляр. У него две краски — белая и чёрная. Зайдя в комнату, маляр перекрашивает её в противоположный цвет. Изначально весь замок выкрашен в белый цвет. Может ли он покрасить его а) в шахматном порядке;
б) «зеброй»? |
 ?
? ?
? ?
?