
МАЛЫЙ МЕХМАТ МГУ

Занятие 5. КОНСТРУКЦИИ
| 1. | Иван-Царевич хочет победить Змея Горыныча, трёхголового и трёххвостого. Баба Яга, подавая Ивану волшебный меч, сказала: «Меч может отрубить за один удар один или два
хвоста, либо одну или две головы. Не забывай, срубишь один хвост — вырастут два хвоста. Срубишь два хвоста — вырастет одна голова.
Одну голову срубишь — одна голова и вырастет, а срубишь две головы — ничего не вырастет. А погибнет Змей только тогда, когда у него ни голов, ни хвостов не останется.» Сможет ли Иван зарубить Змея? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2. | Расставьте в кружках цифры от 1 до 7 так, чтобы сумма вдоль каждой из линий была одинаковой.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3. | Применяя знаки арифметических
действий и скобки, Наташа записала девятью двойками число 200.
А Вы так умеете? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4. | Тетрамино — это многоугольник,
вырезанный из клетчатой бумаги и состоящий из 4 клеток, а пентамино — из 5 клеток. Сколько существует различных а) тетрамино; б) пентамино? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5. | На сковороде могут одновременно жариться 2 котлеты. Каждую надо обжарить с обеих сторон, причём для обжаривания одной стороны требуются 2 минуты. Можно ли поджарить 3 котлеты меньше чем за 7 минут? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6. | Можно ли на шахматной доске расставить а) 9 ладей; б) 14 слонов так, чтобы они не били друг друга? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7. | Разрежьте трёхклеточный уголок на а) 4 равные части; б) 16 равных частей; в) 64 равные части. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8. | Первая слева цифра десятизначного числа равна числу единиц в записи этого числа, вторая — числу двоек, третья — числу троек, четвёртая — числу четверок, ..., девятая — числу девяток, десятая — числу нулей. Найдите это число. Дополнительные задачи | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10. | Расставьте различные натуральные числа в таблице 3×3 так, чтобы произведения в столбцах были равны, и суммы в строках тоже были равны (но суммы могут отличаться от произведений). Домашние задачи | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11. | Может ли в месяце быть а) 3; б) 4; в) 5; г) 6 воскресений? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12. | Найдите путь из левого верхнего угла рисунка до правого нижнего угла (от «а» до «я»), который проходит по одному разу по каждой букве алфавита. (Ходить разрешено только на соседнюю букву по вертикали или горизонтали).
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13. | Есть три сосуда 3 л, 4 л и 5 л без делений, кран с водой, раковина и 3 л сиропа в самом маленьком сосуде. Можно ли с помощью переливаний получить 6 л смеси воды с сиропом так, чтобы в каждом сосуде воды и сиропа стало поровну? |
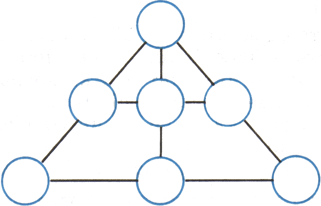
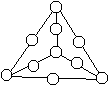 Можно ли расставить в кружочках на рисунке натуральные числа от 1 до 10 так, чтобы сумма чисел по каждому отрезку была одной и той же?
Можно ли расставить в кружочках на рисунке натуральные числа от 1 до 10 так, чтобы сумма чисел по каждому отрезку была одной и той же?