
МАЛЫЙ МЕХМАТ МГУ

Занятие 8. ДЕЛИМОСТЬ
| 1. | Ковбой
Джо приобрел в салуне несколько бутылок кока-колы по 1 доллару 40 центов за штуку, несколько сэндвичей по 35 центов и бифштекс за 2 доллара 80 центов. Бармен сказал, что с него 20 долларов 50 центов. Ковбой Джо достал револьвер.
Как он догадался, что бармена надо перевоспитывать? | |
| 2. | Генерал построил солдат в колонну по 4, но при этом солдат Иванов остался лишним. Тогда
генерал построил солдат в колонну по 5. И снова Иванов остался лишним. Когда же и в колонне по 6 Иванов остался лишним, генерал посулил ему наряд вне очереди, после чего в колонне по 7 Иванов нашёл себе место и никого лишнего не осталось. Какое наименьшее количество солдат могло быть у генерала? | |
| 3. | Можно ли прямоугольник со сторонами 2,3×3,5 см разрезать на прямоугольнички 0,08×0,07 см? | |
| 4. | Докажите, что m3 + 2m делится на 3 для любого натурального m. | |
| 5. | Дети выходят из леса парами. В каждой паре идут мальчик и девочка, причём у мальчика либо в два раза больше орехов, либо в два раза меньше орехов, чем у его девочки. Может ли всего у детей быть 100 орехов? | |
| 6. | Имеются три автомата. Если одному из них на вход дать карточку, где написаны числа | |
| 7. | На поле Чудес растут деревья с золотыми монетами. Каждую ночь на каждом дереве вырастает по одной новой монете. 1 марта на деревьях было всего 1000 монет. В один из дней марта Буратино посадил еще одно дерево, и 31 марта на деревьях оказалось всего 2000 монет. В какой день Буратино посадил дерево? | |
| 8. | Существуют ли два последовательных натуральных числа, сумма цифр каждого из которых делится на 11?
Домашние задачи | |
| 9. | Среди философов каждый седьмой — математик, а среди математиков каждый девятый — философ. Кого больше, математиков или философов? | |
| 10. | Докажите, что | |
| 11. |
|
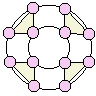 Впишите в кружки 12 последовательных простых чисел от 3 до 41 так, чтобы суммы трёх чисел в вершинах треугольников были равны. Суммы чисел на внутренней и внешней окружностях также должны быть одинаковы.
Впишите в кружки 12 последовательных простых чисел от 3 до 41 так, чтобы суммы трёх чисел в вершинах треугольников были равны. Суммы чисел на внутренней и внешней окружностях также должны быть одинаковы.