МАЛЫЙ МЕХМАТ МГУ

Лекция 1 (110) 2.10.2004

Александр Васильевич СПИВАК,

автор ряда статей журнала «Квант», соросовский учитель школ №№ 1018, 1101 и 1543.

Периодические цепные дроби и квадратичные иррациональности

Цепные дроби позволяют довольно естественным и единообразным способом записать любое вещественное число. Рациональные числа записываются в виде конечных цепных дробей. Любая периодическая цепная дробь, как легко доказать, является квадратичной иррациональностью. Золотое сечение (отношение длины диагонали правильного пятиугольника к длине его стороны) записывается в виде [1; 1, 1, 1, 1, 1, ...]. Корень из двух — в виде [1; 2, 2, 2, 2, 2, ...]. Француз Жозеф Луи Лагранж (1736–1813) доказал, что цепная дробь любой квадратичной иррациональности периодическая. В 1828 году француз Эварист Галуа (1811–1832) выяснил, цепные дроби каких квадратичных иррациональностей периодичны, а каких — имеют предпериод. Оказалось, что квадратичная иррациональность должна быть больше 1, а сопряжённое к ней число должно лежать между –1 и 0.

В следующей таблице даны цепные дроби для квадратных корней из чисел 2, 3, 4, 5, 6, 7, 8, 10, 11,... и наименьшие решения соответствующих уравнений Пелля. Черта выделяет период; как видите, последняя цифра периода в два раза больше целой части квадратного корня из числа n; а если вычеркнуть последнюю цифру периода, то получим палиндром — строку, читаемую слева направо так же, как и справа налево. При помощи вышесформулированной теоремы Галуа легко доказать это интересное свойство и научиться из разложения квадратного корня из данного натурального числа n в цепную дробь получать решение (в натуральных числах) уравнения x² – ny² = ±1.

Лекция 2 (111) 9.10.2004

Александр Ханевич ШЕНЬ,

старший научный сотрудник Института проблем передачи информации РАН, учитель школы номер 57.

Экспонента и логарифм

Вообразите, что мы держим в руке камень и вдруг отпускаем его. Камень падает, скорость его растёт. Как она возрастает: пропорционально пройденному расстоянию, пропорционально времени или по какому-то иному закону? Оказывается, что скорость не может быть пропорциональна пройденному расстоянию ни при каких условиях эксперимента (если только камень не останется висеть неподвижно). Идея проста: половину пути с вдвое меньшей скоростью тело преодолевает за такое же время, как весь путь; таким образом, на любой начальный участок пути камень должен потратить бесконечное время.

Далее был объяснён геометрический смысл задачи: построение графика функции, наклон которого пропорционален ординате соответствующей точки. Время движения проинтерпретировано как площадь под гиперболой. Замечательно, что эта площадь зависит только от отношения ^b/_a. Именно величину этой площади (точнее, величину соответствующего интеграла) и называют натуральным логарифмом числа ^b/_a.

Обратная к логарифму функция — это и есть экспонента. Число, логарифм которого равен 1, обозначают (вслед за Леонардом Эйлером) буквой e. Оказывается, e = lim (1 + ¹/_n)ⁿ. Были обсуждены и другие свойства логарифма, экспоненты и числа e.

Есть брошюра.

Лекция 3 (112) 16.10.2004

Сергей Валерьевич МАРКЕЛОВ,

учитель школы № 57.

Нерешённые проблемы геометрии

В представлениях к полководческим орденам писали: «Смело и решительно обходя очаги сопротивления, не ввязываясь в затяжные бои, проник далеко в глубь обороны противника.» Так и математика ушла далеко вперёд: в некоторых областях, чтобы понять условия задач, нужно учить лет десять специальный язык сложнее китайского. Прорвавшаяся вперёд наука оставила очаги сопротивления даже в элементарной геометрии: точки, прямые, окружности — условия некоторых интересных понятны даже школьнику, а решать их никто не умеет. Вот несколько таких неподдающихся задач.

• Каково минимальное число цветов, в которые можно так раскрасить плоскость, чтобы концы любого отрезка длины 1 были покрашены в разные цвета?
• Существует ли раскраска точек пространства в 14 цветов, при которой концы любого отрезка длины 1 одного цвета?
• Сколько точек общего положения должно быть отмечено на плоскости, чтобы среди них непременно нашлись вершины выпуклого шестиугольника?
• В любом ли многоугольнике с зеркальными изнутри сторонами можно так разместить лампочку, чтобы он был освещён весь?
• Можно ли несколькими кругами, зеркальными снаружи, не пересекающими друг друга и даже не касающимися, загородить горящую лампочку?
• В любом ли многоугольнике с зеркальными сторонами существует хотя бы один замкнутый путь светового луча?
• Существует ли многоугольник, копиями которого плоскость можно покрыть, но только непериодическим образом?
• Может ли выпуклый многогранник, которым можно замостить всё пространство, иметь больше 38 граней?
• Какова фигура минимальной площади, которой можно покрыть любой многоугольник диаметра 1?
• Какова фигура минимальной площади, которой можно покрыть любую фигуру периметра 1?
• Сколь велика может быть площадь n-угольника диаметра 1 при данном n?
• У любого ли выпуклого многогранника существует развёртка без самопересечений?
• Рассмотрим n точек, не лежащих на одной прямой. Обязательно ли среди них найдётся точка, через которую проходит не менее ⁿ/₃ прямых, соединяющих её с остальными n – 1 точками?

Лекция 4 (113) 30.10.2004

Владимир Михайлович ТИХОМИРОВ,

профессор кафедры общих проблем управления мехмата МГУ, заместитель главного редактора журнала «Квант», автор книги «Рассказы о максимумах и минимумах».

Геометрические задачи И.Ф. Шарыгина

Игорь Фёдорович Шарыгин (1937–2004) был выдающимся геометром, автором многих задачников и по математике. Он был замечательным геометрическим композитором, творцом новых геометрических задач. На лекции были обсуждены некоторые геометрические шедевры Шарыгина.

• В треугольнике АВС с углом В величиной сто двадцать градусов проведены биссектрисы АА', BB' и CC'. Чему равна величина угла A'B'C'?
• Четырёхугольник ABCD вписан в окружность. Некоторая окружность с центром на стороне AD касается трёх других сторон. Докажите равенство AB + CD = AD.
• Величины углов BAM и ACM выпуклого четырёхугольника ABMC равны соответственно тридцати и ста пятидесяти градусам. Докажите, что если AB = BC, то AM — биссектриса угла BMC.
• Дан круг единичного радиуса. На диаметре AB дана точка F, через которую проведена хорда CD. Найдите положение хорды, при котором площадь четырёхугольника ACBD максимальна.
• Муха летает внутри правильного тетраэдра с ребром единица. Какое наименьшее расстояние она может пролететь, чтобы побывать на каждой грани и вернуться в исходную точку?

При решении задач были обсуждены, наряду с геометрическими, и алгебраические подходы. Было рассказано о педагогических идеях И.Ф. Шарыгина, о его борьбе за сохранение математического образования в нашей стране, о его воззрениях на геометрию.

Вышла статья: В.Ю. Протасов и В.М. Тихомиров, «Геометрические шедевры Шарыгина», номер 1 «Кванта» 2006 года.

Лекция 5 (114) 6.11.2004

Сергей Александрович ШАРОВ,

архитектор-реставратор.

Надвратный храм Иоакима и Анны во Владимире
(опыт историко-архитектурной реконструкции)

Цель лекции — демонстрация возможностей научной историко-архитектурной реконструкции давно утраченных памятников.

Церковь Иоакима и Анны, построенная епископом Иоанном и князем Всеволодом Большое Гнездо в 1195–1196 годах на воротах детинца города Владимира, давно утрачена. От неё не сохранилось даже изображений (только рисунок воротной башни с надстроенной в XVII веке на месте церкви колокольней), а археологические раскопки выявили лишь основание башни ворот и позволили собрать небольшую коллекцию обломков архитектурных деталей памятника, дающих самое общее представление о его декоративном убранстве. Казалось бы, реконструировать облик храма невозможно.

Однако, особенности техники строительства в полу-бутовой кладке, практически не позволяющей возводить несущие стены толщиной менее 75 см, технические ограничения на отдельные элементы постройки (минимальная ширина дверных проёмов и лестниц, предельный уклон лестницы и т. п.) вкупе с тщательным анализом остатков памятника и его архитектурных аналогов позволяют воссоздать архитектурные формы и структуру утраченной постройки, рассчитать её размеры и осуществить реконструкцию с поразительной точностью (5–10 см).

Полученная реконструкция, в свою очередь, объясняет происхождение ряда загадочных особенностей знаменитых построек Ростовского кремля, возведённых митрополитом Ионой Сысоевичем пятьсот лет спустя, в конце XVII века.

Лекция 6 (115) 13.11.2004

Владимир Игоревич АРНОЛЬД,

академик РАН.

Динамика и статистика полей Галуа

Поле Галуа — это конечное поле. Количество элементов такого поля равно степени простого числа. Поле количеством своих элементов определено однозначно с точностью до изоморфизма. Ненулевые элементы конечного поля образуют циклическую группу по умножению.

Для поля из p² элементов возникает квадратная таблица из p² − 1 натуральных чисел и символа ∞, которые заполняют эту таблицу довольно случайным образом. Вот, например, таблица из 24 чисел:

Постарайтесь угадать, чем эта таблица замечательна. На лекции было рассказано о «случайных» и «неслучайных» свойствах этого заполнения квадрата 5×5 числами и символом бесконечности.

Эти вопросы находятся на границе алгебры, теории чисел, теории динамических систем, теории вероятностей,… Значительная часть фактов, которые были упомянуты, — не теоремы, а эмпирические наблюдения, ожидающие своих исследователей.

Лекция 7 (116) 20.11.2004

Владимир Леонидович НАТЯГАНОВ,

доцент кафедры газовой и волновой динамики мехмата МГУ.

М.В. Ломоносов и загадки атмосферного электричества: сейсмоэлектромагнитные явления

В 1755 году в Европе произошло сильное землетрясение, которое почти полностью разрушило Лиссабон и привело к гибели десятков тысяч людей и многих памятников архитектуры. Эта трагедия породила различные религиозные и философские искания. В научном плане оригинальные и взаимодополняющие ответы дали два самобытных гения: М.В. Ломоносов в России и И. Кант в Германии. Ломоносов в «Слове о рождении металлов от трясения Земли» (1757 год) впервые привёл исчерпывающую характеристику четырёх основных типов колебаний земной поверхности при землетрясениях, высказал ряд правильных гипотез о причинах землетрясений, их роли в образовании различных минералов, кратко описал акустические, гидрологические и световые предвестники землетрясений.

Во второй половине ХХ века инструментально были обнаружены геохимические, сейсмические и электромагнитные предвестники, однако за это время от землетрясений погибло более миллиона человек!

Ибо практически важная и теоретически интересная обратная геофизическая задача — краткосрочный прогноз места и времени будущего землетрясения по многочисленным и противоречивым предвестникам различной природы — всё ещё (уже четверть тысячелетия со времен Ломоносова) так и не решена.

Было рассказано о сейсмоэлектромагнитных явлениях — краткосрочных предвестниках землетрясений электромагнитной природы; возможных физических механизмах вроде гипотезы «подземных гроз» А.А. Воробьёва, лежащих в основе этих эффектов; подходах к их математическому моделированию по аналогии с уже изученными явлениями и процессами (вроде задачи обтекания крыла самолёта воздухом).

Суть лекции можно свести к трём вопросам:

• Почему летают самолеты?
• Когда бывают землетрясения?
• Как образуются алмазы?

Часть ответов на эти малосвязанные на первый взгляд вопросы, может быть, найдут сегодняшние школьники.

Лекция могла быть полезна не только школьникам, но и студентам младших курсов механико-математического, физического факультетов МГУ, а также студентам отделения геофизики геологического факультета.

Литература

• Ломоносов М.В. Избранные произведения. Т.1. Естественные науки и философия. — М.: Наука, 1986.
• Электромагнитные предвестники землетрясений. Под ред. М.А.Садовского.— М.: Наука, 1982.
• Соболев Г.А. Основы прогноза землетрясений. — М.: Наука, 1993.

Лекция 8 (117) 27.11.2004

Владимир Юрьевич ПРОТАСОВ,

кандидат физико-математических наук, преподаватель механико-математического факультета МГУ, автор олимпиадных задач и брошюр по геометрии.

Вокруг теоремы Понселе

В 1822 году французский математик и механик Жан Виктор Понселе опубликовал «Трактат о проективных свойствах фигур», где среди многих других новых геометрических фактов сформулировал теорему о замкнутых ломаных, вписанных в одну окружность и описанных около другой. С этого началась история одной из красивейших теорем планиметрии — теоремы Понселе. Её многократно усиливали и обобщали. Появились и теоремы «в духе Понселе» — так называемые теоремы о замыкании, например, поризм Штейнера (аналог теоремы Понселе для цепочки окружностей, касающихся двух данных окружностей) и «теорема о зигзаге» (иногда называемая «теоремой о блохе»). Интерес к теоремам о замыкании не ослабел и посегодня: за последние годы им было посвящено несколько десятков математических статей. Слушатели познакомились с некоторыми теоремами этого цикла и идеями их доказательств, начиная c классических теорем Понселе и Штейнера и заканчивая современными результатами.

Есть видеозапись 2018-го года и конспект.

Лекция 9 (118) 4.12.2004

Андрей Михайлович РАЙГОРОДСКИЙ,

сотрудник кафедры математической статистики и случайных процессов мехмата МГУ, доктор физико-математических наук, автор брошюры «Хроматические числа» и обзора «Проблема Борсука и хроматические числа метрических пространств» (Успехи математических наук, том 56, номер 1, страницы 107-146).

Разбиения фигур и тел на части меньшего диаметра

Рассмотрим ограниченную фигуру на плоскости. Диаметр фигуры — это максимальное расстояние между парами точек, принадлежащих ей. (Точнее, точная верхняя грань таких расстояний.) В частности, для круга такое понятие диаметра совпадает с общеизвестным. В 1933 году польский математик К. Борсук доказал, что любую фигуру на плоскости можно так разрезать на три «дольки», чтобы диаметр каждой дольки оказался меньше диаметра самой фигуры.

Аналогичной задачей о разрезании тел (шаров, многогранников и тому подобного) на дольки меньшего диаметра естественно заниматься и в пространстве. Более того, можно рассматривать её в пространстве произвольной размерности. Впервые её в общем виде сформулировал Борсук, который поставил знаменитый вопрос: «Верно ли, что всякое ограниченное n-мерное тело может быть разбито на n + 1 часть меньшего диаметра?» Задача проста по формулировке, но исчерпывающего ответа на вопрос Борсука до сих пор нет, хотя он является одним из самых популярных в комбинаторной геометрии.

Было рассказано об интригующей истории задачи, а также приведён ряд интересных и важных вопросов, многие из которых пока открыты.

Вышла брошюра. Есть видеозапись.

Лекция 10 (119) 11.12.2004

Алексей Брониславович СОСИНСКИЙ,

профессор Независимого Московского Университета, директорфранко-русской математической лаборатории, автор многих статей журнала «Квант», брошюры «Узлы и косы» и (в соавторстве с В.В. Прасоловым) монографии «Узлы, косы и трёхмерные многообразия».

Узлы и косы

Известные всем из повседневной жизни понятия узла и косы вдохновили учёных на создание математической теории узлов и кос. На лекции было рассказано о некоторых элементарных геометрических и арифметических аспектах этой теории. Узлы и косы можно не только запутывать и распутывать, но и складывать, умножать.

Лекция была сопровождена компьютерным мультфильмом, созданным Михаилом Юрьевичем Пановым и наглядно показывающим, как выглядят соответствующие операции.

Вышла брошюра: А.Б. Сосинский, «Узлы и косы», выпуск 10 серии «Библиотека "Математическое просвещение"».

Лекция 11 (120) 12.02.2005

Александр Ханевич ШЕНЬ,

кандидат физико-математических наук, старший научный сотрудник Института проблем передачи информации РАН, учитель школы номер 57.

Простые и составные числа

Некоторые факты настолько само собою разумеются, что их в школе доказывать не принято. Один из них — однозначность разложения целых чисел на простые множители. Другой, также обычно не доказываемый факт — бесконечность множества простых чисел. Были рассказаны разные (известные и не очень) доказательства этих утверждений.

Есть брошюра.

Лекция 12 (121) 19.02.2005

Максим Анатольевич ВОЛЧКЕВИЧ,

учитель школы лицея № 2 и гимназии № 1543, автор ряда задач "Задачника «Кванта»" и московской олимпиады.

Параллельная проекция

Как, взглянув на равносторонний треугольник, доказать, что медианы любого треугольника пересекаются в одной точке?

Почему нельзя при помощи одной только линейки опустить перпендикуляр на данную прямую?

Как параллельная проекция помогает при решении стереометрических задач?

Теорема Дезарга и её следствия. Как соединить две удалённые точки при помощи короткой линейки?

Произвольный выпуклый четырёхугольник можно получить параллельной проекцией из некоторого четырёхугольника, два угла которого прямые. При помощи этого наблюдения нетрудно доказать теорему о прямой Гаусса и другие интересные факты.

Эллипс — параллельная проекция круга. Как выразить площадь эллипса через длины его полуосей? Что является тенью шара? Какова форма месяца (Луны на звёздном небе)? Что можно сказать об основании наклонной призмы, если в неё можно вписать шар?

Для любого чётноугольника, описанного около эллипса, сумма величин углов, под которыми из центра эллипса видны стороны, взятые через одну, равна 180 градусам.

При помощи параллельной проекции были доказаны теоремы Ньютона и Брианшона.

Разумеется, изложить и тем более доказать столько теорем на одной лекции невозможно. Поэтому лектор завершил свой рассказ 19 марта.

Лекция 13 (122) 26.02.2005

Григорий Вячеславович КОНДАКОВ,

кандидат физико-математических наук, заместитель директора Дворца научно-технического творчества молодёжи.

Теорема Ван дер Вардена об арифметической прогрессии

Если натуральный ряд каким угодно способом разбит на несколько подмножеств, то хотя бы в одном из этих подмножеств есть сколь угодно длинная арифметическая прогрессия. Эта теорема была доказана в 1928 году голландцем Ван дер Варденом. Доказательство можно найти в книге А.Я. Хинчина «Три жемчужины теории чисел».

Лекция 14 (123) 5.03.2005

Александр Николаевич КАРПОВ,

кандидат физико-математических наук, ассистент кафедры общей топологии механико-математического факультета МГУ, заместитель директора Малого мехмата, учитель лицея № 2 и школы № 17.

Теорема Морлея о трисектрисах

Разбив каждый угол треугольника на три равные части и рассмотрев, как показано на рисунке, их точки пересечения, мы получим равносторонний треугольник. Это доказал в 1904 году Франк Морлей.

Доказательство можно найти в книге Г.С.М. Коксетера и С.Л. Грейтцера «Новые встречи с геометрией».

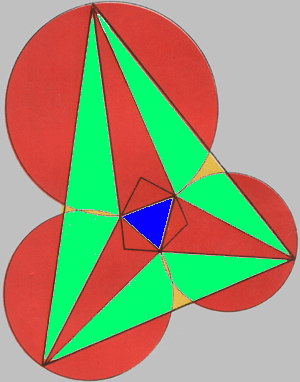
Лекция 15 (124) 12.03.2005

Владимир Михайлович ТИХОМИРОВ,

профессор кафедры ОПУ мехмата МГУ, заместитель главного редактора журнала «Квант», автор книги «Рассказы о максимумах и минимумах».

Теоремы существования

Теорема Коши о промежуточном значении непрерывной функции, теорема Вейерштрасса о наибольшем и наименьшем значениях непрерывной функции на отрезке (и вообще на любом ограниченном замкнутом множестве), теорема Брауэра о неподвижной точке непрерывного отображения отрезка (круга, шара) в себя, метод Ньютона решения уравнений, основная теорема алгебры (гласящая, что любой многочлен, отличный от константы, имеет хотя бы один комплексный корень), существование неалгебраических чисел, несчётность континуума.

Была издана брошюра: В.М. Тихомиров, «Дифференциальное исчисление (теория и приложения)», выпуск 15 серии «Библиотека "Математическое просвещение"» (есть и djvu-файл.)

Лекция 16 (125) 19.03.2005

Максим Анатольевич ВОЛЧКЕВИЧ,

учитель школы лицея № 2 и гимназии № 1543, автор ряда задач "Задачника «Кванта»", московской и соросовской олимпиад.

Параллельная проекция

Это окончание лекции, первая часть которой была 19 февраля 2005 года.

Лекция 17 (126) 26.03.2005

Светлана Анатольевна БУРЛАК,

кандидат филологических наук, старший научный сотрудник Института востоковедения РАН, член оргкомитета Московской олимпиады по лингвистике и математике, автор многих олимпиадных задач по лингвистике.

Математика в задачах по лингвистике

Было рассказано о том, чем занимается современная лингвистика, о проблемах и методах исследования, о роли математики и математиков в развитии отечественной лингвистики. Основная часть лекции посвящена лингвистическим задачам и лингвистической олимпиаде.

Что такое лингвистическая задача, чем она похожа на математическую и чем отличается от неё? Какие бывают задачи? Какие языковые явления они затрагивают? Обязательно ли знать китайский язык, чтобы решить задачу, начинающуюся с «Даны следующие китайские существительные...»? Как решать лингвистические задачи? Чем помогает при этом математика (метод установления корреляций, матричный метод и другие)? Что такое паразитическое решение и как с ним бороться? Как составить лингвистическую задачу, чтобы она имела единственное решение?

Лекция 18 (127) 2.04.2005

Виктор Александрович МАТЮХИН,

младший научный сотрудник ВМК МГУ, учитель информатики гимназии 1543, председатель методической комисии московской олимпиады по информатике, председатель научного комитета и член жюри Всероссийской олимпиады школьников по информатике, тренер сборной России к международной олимпиаде школьников по информатике.

Сложности алгоритмов

• Что такое сложность алгоритма?O и o-символика. Почему сложность измеряют «с точностью до констант»?
• Примеры алгоритмов и их сложности. Структуры данных и сложности алгоритмов. Бинарный поиск в отсортированном массиве. Поиск кратчайшего пути в графе. Матрица смежности, список рёбер графа.
• NP-полные задачи. Что такое вычислимость за полиномиальное время? Примеры NP-полных задач. Полиномиальное сведение одной задачи к другой. Можно ли решить NP-полную задачу «без перебора», точнее, можно ли решить такую задачу за полиномиальное время?
• Алгоритмическая неразрешимость. Невозможность выяснить, остановится ли работающая программа или будет работать бесконечно долго.

Лекцию для школьников хотел прочитать и Алексей Фёдорович ФИЛИППОВ, профессор кафедры дифференциальных уравнений механико-математического факультета МГУ. Из-за его болезни лекция не состоялась. Тем не менее, читатель сайта может ознакомиться с темой, аннотацией и даже полным текстом лекции А.Ф. Филиппова. (Доступна и Word-версия.) Тема несостоявшейся лекции: «Как сложились научные представления об окружающем мире?»

1. Что такое наука. Развитие геометрии и астрономии.
   Как в древности измерили земной шар?
   
2. Великие географические открытия.
   Развитие астрономии. Открытия с помощью микроскопа и телескопа.
   Ньютон — основатель теоретической механики и высшей математики.
   Химия и алхимия. Закон сохранения вещества.
   Паровая машина Уатта — основной двигатель техники 19 века.
   Классификация Линнея животных и растительных видов.
   
3. Геологические силы, меняющие поверхность Земли.
   Дальтон и современные теоретические взгляды в химии.
   Связь электричества и магнетизма.
   Закон сохранения энергии.
   Периодическая система химических элементов.
   Эволюция животных и растений.
   Общая теория электромагнитных явлений. Радиоволны.
   Электролитическая диссоциация.
   Картина мира к концу 19 века.
   
4. Радиоактивность. Двойственная природа света.
   Модель атома, предложенная Бором.
   Теория относительности Эйнштейна.
   Теория движения материков.
   Квантовая механика. Новые элементарные частицы.
   Деление атомов урана. Атомные бомбы и реакторы.
   Полупроводниковые диоды и триоды, их применения.
   Ракеты космические и военные.
   Генетика. Химический состав наследственного вещества.
   Технические достижения.
   Влияние человека на окружающую среду.
   

Лекция 19 (128) 9.04.2005

Алексей Андреевич Панов,

кандидат физико-математических наук, преподаватель Московского университета геодезии и картографии (бывший МИИГАиК).

Радуга Декарта и радуга Ньютона

Радуга — это гигантский оптический эксперимент, который демонстрирует нам природа всякий раз, как только удалённая от нас стена дождя освещена низко стоящим Солнцем.

Первая последовательная теория радуги была построена Декартом. Используя только что открытый закон преломления и проведя многочисленные расчёты, Декарт выяснил, как образуется радуга (Discours de la méthode, 1637 год).

В 1802 году Томас Юнг открыл явление интерференции света и тем самым подтвердил волновую природу света. Волновая теория позволила по-новому взглянуть на механизм образования радуги и дополнить декартову теорию радуги недостающими деталями.

Лекция 20 (129) 16.04.2005

Андрей Михайлович РАЙГОРОДСКИЙ,

сотрудник кафедры математической статистики и случайных процессов мехмата МГУ, доктор физико-математических наук, автор брошюры «Хроматические числа» и обзора «Проблема Борсука и хроматические числа метрических пространств» (Успехи математических наук, том 56, номер 1, страницы 107-146).

Остроугольные треугольники Эрдёша и Фюреди

В 1962 году Людвиг Данцер и Бранко Грюнбаум предложили выяснить, насколько много точек может содержать такое множество точек в евклидовом пространстве Rⁿ, что все треугольники с вершинами в этом множестве остроугольные. Несложно придумать такое множество из 2n – 1 точек. Авторы задачи думали, что лучшей конструкции не бывает. Гипотеза продержалась более двадцати лет. Пол Эрдёш и Золтан Фюреди с помощью весьма изящной комбинаторики её опровергли. Оказалось, существует такое множество из [cⁿ/2] точек, где c² = ⁴/₃.

Дмитрий Захаров, будучи учеником 10-го класса, в 2017-м году построил пример множества точек в n-мерном пространстве, в котором не менее 2^n/2 остроугольных треугольников.

Вышла брошюра: А.М. Райгородский, «Остроугольные треугольники Данцера–Грюнбаума», выпуск 36 серии «Библиотека "Математическое просвещение"».

Есть видеозапись 2018-го года.

Лекция 21 (130) 23.04.2005

Дмитрий Евгеньевич КОСОВ,

студент 2 курса мехмата МГУ, соавтор статей «Траектории замечательных точек треугольника Понселе» и «Сравнительная геометрия треугольника и тетраэдра».

Теоремы Дезарга, Паскаля и Брианшона

Красота проективной геометрии была продемонстрирована на примере классических теорем геометрии — теорем Дезарга, Паскаля и Брианшона. Особое внимание было уделено важному принципу проективной геометрии — принципу двойственности.

Лекция 22 (131) 30.04.2005

Евгений Владимирович АДИЩЕВ,

преподаватель МММФ.

Функциональные уравнения

В школе изучают уравнения, в которых нужно найти некоторое число. В математике встречаются и уравнения, где неизвестной является функция. Такие уравнения называются функциональными. На примере двух (похожих по виду, но различающихся по сложности) уравнений

были рассмотрены методы решения функциональных уравнений. Слушатели познакомились также с понятиями орбиты, цикла и сопряжения.