МАЛЫЙ МЕХМАТ МГУ

Лекция 1 (245) 18.09.2010

Виктор Васильевич ПРАСОЛОВ,

автор книг «Геометрия Лобачевского», «Задачи по планиметрии», «Задачи по алгебре, арифметике и анализу», «Многочлены», «Наглядная топология», «Точки Брокара и изогональное сопряжение», «Элементы комбинаторной и дифференциальной топологии», «Элементы теории гомологий», соавтор (с А.Б. Сосинским) книги «Узлы, зацепления, косы и трёхмерные многообразия» и соавтор (с В.М. Тихомировым) книги «Геометрия».

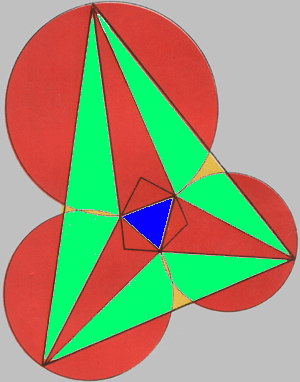
Теорема Морли

Теорема Франка Морли утверждает, что при пересечении трисектрис углов любого треугольника образуется правильный треугольник. Были рассказаны сравнительно простые доказательства этой теоремы, появившиеся не так давно.

Доказательство можно найти в книге Г.С.М. Коксетера и С.Л. Грейтцера «Новые встречи с геометрией».

Лекция 2 (246) 25.09.2010

Алексей Александрович ЗАСЛАВСКИЙ,

старший научный сотрудник ЦЭМИ РАН, председатель жюри Всероссийской олимпиады по геометрии имени И.Ф. Шарыгина.

Точки Микеля

Пусть даны четыре прямые общего положения. Тогда четыре окружности, описанные около образованных ими треугольников, пересекаются в одной точке, которая называется точкой Микеля.

Рассмотрим теперь четыре точки. Соединяя их в разном порядке, можно получить три различных четырёхугольника (возможно, самопересекающихся). Стороны каждого из этих четырёхугольников определяют свою точку Микеля. Полученная конфигурация обладает рядом красивых свойств. Они были обнаружены П. Кожевниковым, Н. Белуховым и автором. Изучались на Летней конференции Турнира городов в августе 2010 года.

Лекция 3 (247) 2.10.2010

Юрий Викторович САДОВНИЧИЙ,

профессор кафедры общей топологии и геометрии мехмата МГУ, доктор физико-математических наук, автор книг и пособий для школьников.

Углы, окружности и подобные треугольники

Был изложен теоретический материал и рассмотрены интересные (в том числе и сложные) задачи, касающиеся равенств углов, а также отношений длин отрезков, которые из этих равенств вытекают. Можете ознакомиться с условиями и решениями этих задач.

Лекция 4 (248) 9.10.2010

Игорь Николаевич МОЛОДЦОВ,

заместитель декана мехмата МГУ, профессор.

Математика в Московском университете

В рамках «Фестиваля науки» И.Н. Молодцов выступил перед школьниками и их родителями.

Лекция 5 (249) 16.10.2010

Александр Васильевич СПИВАК,

автор книг «1001 задача по математике», «Математический кружок», «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и «Арифметика—2», преподаватель Малого мехмата, учитель школ №№ 1018 и 1543.

Перестановки, пары таблиц Юнга и максимальные монотонные подпоследовательности

Было рассказано о связи между перестановками и таблицами Юнга и доказано, что для любых натуральных чисел m и n в любой перестановке mn + 1 чисел есть убывающая подпоследовательность длины m + 1 или возрастающая подпоследовательность длины n + 1.

Лекция 6 (250) 23.10.2010

Александр Васильевич СПИВАК,

автор книг «1001 задача по математике», «Математический кружок», «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и «Арифметика—2», преподаватель Малого мехмата, учитель школ №№ 1018 и 1543.

Ловушка для треугольника

В третьем номере «Кванта» 1999 года опубликована статья В.Н. Дубровского и В.А. Сендерова «Ловушка для тругольника». В ней рассказано о том, как находить расстояния между замечательными точками треугольника и почему корнями уравнения

x³ – px² + (r² + 4rR)x = r²p,

где p — полупериметр, а r и R — соответственно, радиусы вписанной и описанной окружностей, являются числа p – a, p – b и p – c, где a, b и c — длины сторон треугольника. Именно при помощи этого уравнения легко доказать существование треугольника, ортоцентр (точка пересечения высот) и центр тяжести (точка пересечения медиан) которого лежат на его вписанной окружности.

Лекция 7 (251) 30.10.2010

Александр Васильевич СПИВАК,

автор книг «1001 задача по математике», «Математический кружок», «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и «Арифметика—2», преподаватель Малого мехмата, учитель школ №№ 1018 и 1543.

Перестановки и пары таблиц Юнга

Окончание лекции, прочитанной 16 октября 2010 года. Было рассказано о свойствах таблиц Юнга. Полезно прочитать статью «Формула крюков» третьего номера «Кванта» 2009 года.

Лекция 8 (252) 6.11.2010

Фёдор Константинович НИЛОВ,

студент III курса мехмата МГУ.

Новый взгляд на коники

Хорошо известны два определения эллипса с помощью двух фокусов (множество точек, сумма расстояний до которых равна данной величине) и фокуса с директрисой (множество точек, расстояние от которых до фокуса равно произведению эксцентриситета, который меньше единицы, на расстояние до данной прямой, называемой директрисой). Основная мысль лекции состояла в том, что в этих определениях фокусы можно заменять на окружности, а расстояние от точки до фокуса — на длину касательной:

Аналогичные определения можно дать для гипербол и парабол.

Были рассказаны два применения этих определений. Рассмотрим две окружности ω₁ и ω₂, причём ω₂ лежит строго внутри ω₁. Рассмотрим множество E эллипсов, каждый из которых вписан в ω₁ (касается в двух точках) и описан около ω₂. Тогда все эллипсы из E подобны; их фокусы лежат на одной окружности, концентричной с ω₁; для любых двух эллипсов из E диагонали криволинейного четырёхугольника, образованного их пересечением, перпендикулярны:

Другим применением является обобщение конструкции шаров Данделена на случай эллипсоида вращения.

Лекция 9 (253) 13.11.2010

Светлана Анатольевна БУРЛАК,

кандидат филологических наук, старший научный сотрудник Института востоковедения РАН и филологического факультета МГУ, член оргкомитета Московской олимпиады по лингвистике и математике, автор многих олимпиадных задач по лингвистике.

Лингвистические задачи

Стало традицией незадолго до Традиционной лингвистической олимпиады знакомить школьников — слушателей лектория Малого мехмата — с тем, что такое лингвистика, демонстрировать примеры лингвистических задач. Задачи лингвистической олимпиады самодостаточны — это значит, что для их решения не нужны специальные знания, достаточно лишь уметь логически рассуждать. В этом лингвистика похожа на математику: при описании языка требуется доказывать каждое предположение. Как и в прошлые годы, говорили о том, что такое язык и как его описывают. Но задачи, разумеется, были новые!

Если вам нравится разбираться в устройстве языка — добро пожаловать на Традиционную лингвистическую олимпиаду.

Лекция 10 (254) 20.11.2010

Олег Николаевич ГЕРМАН,

доцент кафедры теории чисел, преподаватель СУНЦ МГУ.

Геометрия цепных дробей

Цепные дроби — математическая конструкция, в скрытом виде встречающаяся в самых неожиданных местах: от формата А4 до переговорного устройства в лифтах МГУ. Обычно цепные дроби определяют при помощи алгебры, мы же рассмотрели этот объект с геометрической точки зрения. Методы геометрии чисел позволяют доказать многие фундаментальные свойства цепных дробей и классические теоремы.

Лекция 11 (255) 27.11.2010

Сергей Владимирович ДВОРЯНИНОВ,

кандидат физико-математических наук, доцент, автор статей журналов «Квант», «Потенциал», «Математическое образование», «Математика в школе», «Математика для школьников» и газеты «Математика».

Об одном математическом случае, или Штопор и бифуркации

На уроках математики решают задачи с параметрами. В физике изучают положения равновесия. Пример — детские качели. «Нелинейные» качели интереснее обычных: при разных значениях параметра уравнение может иметь разное количество корней. При изменении параметров механической системы положения равновесия могут исчезать и появляться. Подобные явления называют бифуркациями. Бифуркации были проиллюстрированы при помощи штопора. Было рассказано о статье «Об одном математическом случае», опубликованной в четвёртом и пятом номерах «Кванта» 2005 года.

Лекция 12 (256) 4.12.2010

Александр Владимирович ЖУКОВ,

ведущий рубрики «"Квант" для младших школьников» журнала «Квант» в 1998–2007 годах, автор книги «Вездесущее число π»

«Экспериментальная математика»

Компьютерная графика — сравнительно молодое направление экспериментальной математики. Компьютер может стать чудодейственным инструментом, позволяющим увидеть многие закономерности. На примере простейших алгоритмов («стежок», о котором рассказано в пятом номере «Кванта» 1992 года, а также различные отображения натурального ряда и динамические модели) были проиллюстрированы как широко известные, так и ещё до конца не изученные свойства чисел.

Лекция 13 (257) 11.12.2010

Александр Васильевич СПИВАК,

автор книг «1001 задача по математике», «Математический кружок», «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и «Арифметика—2», преподаватель Малого мехмата, учитель школ №№ 1018 и 1543.

Инверсия и построения одним циркулем

Было рассказано о том, что такое инверсия, показана её связь со стереографической проекцией. Были доказаны важнейшие свойства инверсии и неожиданная теорема: линейка не нужна для геометрических построений! (Конечно, прямую без линейки не проведёшь, но если задавать прямую при помощи пары точек на ней, то линейка действительно не нужна!)

Лекция 14 (258) 18.12.2010

Александр Васильевич СПИВАК,

автор книг «1001 задача по математике», «Математический кружок», «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и «Арифметика—2», преподаватель Малого мехмата, учитель школ №№ 1018 и 1543.

Задача Аполлония

Как по трём данным окружностям (в роли каждой из которых может выступить и точка, и прямая) построить окружность или прямую, касающуюся всех трёх? Эта и многочисленные другие задачи на построение могут быть решены при помощи инверсии.

Лекция 15 (259) 12.02.2011

Александр Васильевич СПИВАК,

автор книг «1001 задача по математике», «Математический кружок», «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и «Арифметика—2», учитель школ №№ 1018 и 1543.

Избранные задачи Всесоюзных олимпиад

Было рассказано о недавно переизданной книге «Задачи Всесоюзных олимпиад» и разобрано несколько очень красивых задач.

Лекция 16 (260) 19.02.2011

Александр Васильевич СПИВАК,

автор книг «1001 задача по математике», «Математический кружок», «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и «Арифметика—2», учитель школ №№ 1018 и 1543.

Бесповторные последовательности

Слово Туэ задано очень простым рекуррентным правилом, однако оно приводит к явному примеру бесквадратной последовательности букв трёхбуквенного алфавита. Можно доказать существование бесконечного бесповторного слова и другим способом, о котором тоже было рассказано.

Есть видеозапись.

Лекция 17 (261) 26.02.2011

Александр Васильевич СПИВАК,

автор книг «1001 задача по математике», «Математический кружок», «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и «Арифметика—2», учитель школ №№ 1018 и 1543.

Площади прямоугольных треугольников. Метод бесконечного спуска

Не существует ни одного прямоугольного треугольника, длины всех сторон которого — рациональные числа, а площадь равна 1. Не может площадь равняться и 2, и многим другим числам. Лекция посвящена методу бесконечного спуска, который позволяет доказывать факты такого рода.

Есть видеозапись.

Лекция 18 (262) 5.03.2011

Сергей Владимирович ДВОРЯНИНОВ,

кандидат физико-математических наук, доцент, автор статей журналов «Квант», «Потенциал», «Математика для школьников», «Математика в школе», «Математическое образование» и газеты «Математика».

Об итерациях в геометрии, о предельных циклах и их бифуркациях

ИТЕРАЦИЯ (от латинского iteratio — повторение) — многократное применение какой-либо математической операции. Итерации возникают, например, в задаче построения общего перпендикуляра к двум скрещивающимся прямым линиям в пространстве. Предельный цикл возникает при переходе с одной стороны правильного треугольника на другую по перпендикуляру.

Лекция 19 (263) 19.03.2011

Александр Васильевич СПИВАК,

автор книг «1001 задача по математике», «Математический кружок», «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и «Арифметика—2», учитель школ №№ 1018 и 1543.

Теорема Холла о различных представителях, или Деревенские свадьбы

Одна из важнейших теорем комбинаторики — теорема Холла о различных представителях, она же — теорема о сватовстве. Она помогает решать довольно разнообразные задачи и многократно переоткрывалась в разных конкретных ситуациях.

Есть видеозапись.

Лекция 20 (264) 26.03.2011

Дмитрий Викторович ШВЕЦОВ,

учитель школы №179.

От средней линии треугольника до прямой Эйлера четырёхугольника

Прямая Эйлера и окружность девяти точек треугольника довольно известны любителям элементарной геометрии. Аналогичные объекты для четырёхугольника гораздо менее популярны. Мы восполним этот пробел. Для понимания достаточно знать теорему о средней линии треугольника и свойства вписанных углов.

Лекция 21 (265) 2.04.2011

Владимир Викторович ТРУШКОВ,

преподаватель Костромской летней многопредметной школы, Курганской летней математической школы, преподаватель Университета города Переславля.

Лемма Турана

Специалистов по теории графов часто интересует вопрос: как наибольшее количество рёбер может быть в графе на n вершинах, удовлетворяющем некоторому свойству? Например, каким может быть число рёбер в графе, не содержащем заданного подграфа H? Впервые такую задачу поставил в 1941 году венгерский математик Пал Туран (1910–1976), который решил её, когда H — полный подграф на m вершинах. Было рассказано решение этой задачи и обсуждён случай, когда H — полный двудольный граф (каждый из r домов соединён с каждым из s колодцев). Применение этой теории было проиллюстрировано на многих задачах разных олимпиад:

• 22 школьника участвовали в съезде юных писателей. После съезда каждый из них прочитал произведения трёх юных писателей, побывавших на съезде. Докажите, что из делегатов съезда можно составить комиссию из 4 человек так, что в комиссии никто не читал произведения остальных её членов.
• В группе из n² человек каждый имеет не более n знакомых среди остальных. Докажите, что можно выбрать n человек, никакие двое из которых не знакомы друг с другом.
• В коллективе из 30 человек любых троих можно усадить за круглый стол таким образом, что каждый будет сидеть со своим знакомым. Докажите, что в этом коллективе найдётся компания из 10 человек, в которой каждый знаком с каждым.
• В графе на 300 вершинах степень каждой вершины не менее 190. Докажите, что можно выбрать 25 треугольников, никакого два из которых не имеют ни одной общей вершины.
• В кружке 20 учеников. Среди них есть ученик, имеющий среди кружковцев одного друга; ученик, имеющий среди кружковцев двоих друзей; ...; ученик, имеющий среди кружковцев 14 друзей. Докажите, что найдутся трое кружковцев, каждые два из которых дружат.
• В графе 34 вершины, степень каждой не менее 4, и для каждой вершины есть ровно одна вершина той же степени. Докажите, что в этом графе есть три вершины, попарно соединённые ребрами.
• На конгресс приехало 100 ученых, каждый из которых сделал доклад. В конце каждый заявил, что ему понравилось не менее 83 докладов, сделанных его коллегами. Докажите, что найдутся четверо, каждому из которых понравились доклады двух других.
• В стране 210 городов и совсем нет дорог. Король хочет построить несколько дорог с односторонним движением так, чтобы для любых трёх городов A, B, C, между которыми есть дороги, ведущие из A в B и из B в C, не было бы дороги, ведущей из A в B. Какое наибольшее число дорог он сможет построить?
• Рёбра графа на 300 вершинах покрашены в красный и синий цвета так, что нет ни одного одноцветного треугольника. Какое наибольшее число рёбер может быть в таком графе?

Лекция 22 (266) 9.04.2011

Александр Васильевич СПИВАК,

автор книг «1001 задача по математике», «Математический кружок», «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и «Арифметика—2», учитель школ №№ 1018 и 1543.

Теорема об арифметической прогрессии и числа Рамсея

Если натуральный ряд раскрасить в два цвета, то найдётся сколь угодно длинная арифметическая одноцветная прогрессия. Если рёбра полного графа на 17 вершинах раскрашены в 3 цвета, то найдётся одноцветный треугольник.

Есть видеозапись 2013-го и 2015-го годов.

Лекция 23 (267) 16.04.2011

Александр Васильевич СПИВАК,

автор книг «1001 задача по математике», «Математический кружок», «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и «Арифметика—2», учитель школ №№ 1018 и 1543.

Почему не уменьшается сопротивление?

При увеличении сопротивления любого провода электрической цепи постоянного тока (например, при перерезании этого провода) сопротивление цепи не может уменьшиться. Эта очевидная для любого физика теорема нуждается в математическом доказательстве. Доказательство основано на рассмотрении квадратичной функции многих переменных: энергии, выделяемой при протекании тока по цепи. Прочитать его можно в первом номере журнала «Квант» 1985 года.

Есть видеозапись 2016-го года:
1. «Потенциалы, закон Кирхгофа, альтернатива Фредгольма»;
2. «Мощность и точка минимума квадратичной функции»;
3. «Разрезания металлического прямоугольника».

Лекция 24 (268) 23.04.2011

Александр Васильевич СПИВАК,

автор книг «1001 задача по математике», «Математический кружок», «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и «Арифметика—2», учитель школ №№ 1018 и 1543.

Дерево Калкина-Вилфа

Множество точек плоскости с натуральными координатами счётно. Счётно и положительных рациональных чисел. В обоих случаях взаимно-однозначное соответствие задаётся очень естественным и красивым способом. Советую статью «По порядку становись!» второго номера журнала «Квант» 2008 года.

Есть видео.

Лекция 25 (269) 30.04.2011

Александр Васильевич СПИВАК,

автор книг «1001 задача по математике», «Математический кружок», «Математический праздник», «Турниры математических боёв имени А.П. Савина», «Арифметика» и «Арифметика—2», учитель школ №№ 1018 и 1543.

Гармонический ряд, или Собака бежит наперерез

Сумма величин, обратных первым n натуральным числам, стремится к бесконечности при возрастании n. А сумма ряда обратных квадратов конечна. В статье М.Л. Гервера «Собака бежит наперерез» третьего номера «Кванта» 1973 года из этих фактов выведено решение задачи Радо о дрессировщике, убегающем на арене цирка от льва, скорость которого в точности равна скорости дрессировщика.

Было рассказано и содержание статьи М.Л. Гервера «Про лису и собаку» второго номера «Кванта» 1973 года.