МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Математическая регата (30.10.2004)

Блок 1 (10 мин) (каждая задача — 6 баллов)

1-1.

Решите уравнение ((x : 2 – 3) : 2 – 1) : 2 – 4 = 3.

Ответ Решение

Ответ. 66

Решение. x = (((3 + 4) · 2 + 1) · 2 + 3) · 2 = 66.

1-2.

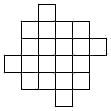Разрежьте фигуру, изображённую на рисунке, на четыре равные части так, чтобы линии разрезов шли по сторонам клеток. Найдите как можно больше способов. (Симметричные случаи различными не считаются.)

Комментарий

Комментарий. Всего существует шесть различных способов.

1-3.

У зайцев было несколько бревен. Все бревна были распилены: всего сделали 20 распилов и получили 27 чурбачков. Сколько бревен было у зайцев? (Ответ объясните.)

Ответ Решение

Ответ. 7 брёвен.

Решение. Рассмотрим процесс распиливания брёвен. Каждый раз при распиле образуется минимум один чурбачок, который больше никогда не будут распиливать. Можно считать, что такие чурбачки — это правые концы брёвен. Предположим, что зайцы каждый раз, делая очередной распил, правый конец бревна складывали в отдельную поленницу. Тогда после 20 распилов в этой поленнице оказалось 20 чурбачков и ещё семь чурбачков остались не сложенными. А эти семь чурбачков могли быть только самыми левыми концами брёвен, поэтому они все отпилены от разных брёвен.

Блок 2 (15 мин.) (каждая задача — 7 баллов)

2-1.

Решите ребус: A + BB + A = CCC. (Каждую букву надо заменить цифрами, при этом одинаковым буквам соответствуют одинаковые цифры, а разным буквам — разные цифры.) Найдите все решения и объясните, как вы нашли ответ.

Ответ Решение

Ответ. 6 + 99 + 6=111

Решение. Даже если к самому большому двузначному числу 99 прибавить два самых больших однозначных числа 9, получится 117. Значит, С = 1. Если BB = 99, то A = (111 − 99) / 2 = 6. Если BB = 88 или меньше, то A = (111  − 88) / 2 = 11,5 или больше, что невозможно, т. к. A — цифра. Значит, есть только одно решение: A = 6, B = 9 и C = 1.

2-2.

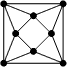
Нарисуйте восемь точек и соедините их отрезками так, чтобы отрезки не пересекались и каждая точка была бы вершиной ровно четырёх отрезков.

Решение

Решение.

2-3.

Жители города А говорят только правду, жители города В — только ложь, а жители города С — попеременно правду и ложь (т. е. из двух высказанных ими утверждений одно истинно, а другое ложно). В пожарную часть сообщили по телефону: «У нас пожар, скорее приезжайте!» «Где?» — спросил дежурный по части. «В городе С», — ответили ему. В какой город должна приехать пожарная машина?

Ответ: Решение

Ответ:. В город А.

Решение. Из города А позвонить не могли, так как первое и второе утверждение противоречили бы друг другу. Из города C позвонить тоже не могли, так как тогда утверждения имеют одинаковый смысл, и, соответственно, должны быть или оба истинны или оба ложны, что невозможно для жителей города C. Значит, звонили из B. Поэтому пожар не в B и не в C, значит, если пожар и есть, то в городе A.

Блок 3 (20 мин.) (каждая задача — 8 баллов)

3-1.

Было два положительных числа. Одно из них увеличили на 1 процент, второе — на 4 процента. Могла ли их сумма увеличиться на 3 процента? (Если да, приведите пример, если нет — объясните, почему.)

Ответ Решение

Ответ. Да, могла

Решение. Рассмотрим, например, числа 100 и 200. Первое увеличилось на 1, второе — на 8. Их сумма увеличилась на 9, что как раз составляет 3% от трёхсот.

3-2.

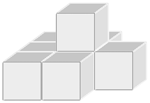
Как на стол поставить 8 одинаковых кубиков так, чтобы со всех сторон полностью было видно ровно 23 грани кубиков, а остальные грани видны не были?

Решение

Решение.

3-3.

В колонию, состоящую из двухсот бактерий, попадает один вирус. В первую минуту он уничтожает одну бактерию, затем делится на два новых вируса, и одновременно каждая из оставшихся бактерий тоже делится на две новые. В следующую минуту возникшие два вируса уничтожают две бактерии, и затем каждый из оставшихся вирусов и каждая из оставшихся бактерий снова делятся пополам и так далее. Будет ли эта колония жить бесконечно долго или, если она в конце концов погибнет, то через какое время это произойдёт?

Ответ Решение

Ответ. Колония погибнет через 200 минут.

Решение. Поскольку и вирусы, и бактерии делятся пополам, можно считать, что у каждого вновь образовавшегося вируса «своя» вновь образовавшаяся колония бактерий, и эта колония идентична колониям всех остальных вирусов, поэтому все процессы в колониях разных вирусов будут происходить одинаково. У первого вируса в «его» колонии сначала было 200 бактерий, и каждую минуту он уничтожал по одной бактерии (каждую минуту при этом отпочковывались новые вирусы вместе со своими колониями, которые представляли собой точные копии этой). Значит, этот вирус ровно за двести минут уничтожил всех «своих» бактерий, а поскольку во всех колониях в любой момент времени одинаковое количество бактерий, то через двести минут бактерий не останется вовсе.

Блок 4 (25 мин.) (каждая задача — 9 баллов)

4-1.

Над цепью озер летела стая гусей. На каждом озере садилась половина гусей и еще полгуся, а остальные летели дальше. Все гуси сели на 8 озерах. Сколько гусей было в стае?

Ответ Решение

Ответ. 255 гусей

Решение. На последнем озере сели половина всех и еще 0,5, т.е. 0,5 — это половина, значит, сел один гусь. На седьмом озере сели половина всех, и осталось 1,5 гуся, значит, все — это 3 гуся. На шестом озере сели половина и осталось 3,5, значит, все — это 7 гусей. На пятом озере сели половина и осталось 7,5, значит, все — это 15 гусей. На четвёртом озере сели половина и осталось 15,5, значит, все — это 31 гусь. На третьем было 63 гуся, на втором озере — 127 гусей, и на первом — 255.

4-2.

Каждая точка плоскости покрашена либо в красный, либо в синий цвет. Докажите, что обязательно найдутся две точки одного цвета, расстояние между которыми ровно 1 метр.

Решение

Решение. Рассмотрим три точки, образующие треугольник со сторонами 1, 1, 1. Из этих трёх точек по крайней мере две одного цвета и находятся на расстоянии 1.

4-3.

За круглым столом сидят 7 дипломатов. Они должны провести по одной беседе друг с другом. Два дипломата будут беседовать только в том случае, если они окажутся рядом. После того, как каждый из дипломатов закончил переговоры со своими соседями, дипломаты встают и занимают новые положения. С каким минимальным количеством пересаживаний может пройти встреча?

Ответ Решение

Ответ. С тремя пересаживаниями.

Решение. Меньше трёх быть не может, так как всего бесед 6 + 5 + 4 + 3 + 2 + 1=21, а за один круглый стол пройдёт только 7 бесед. А три можно следующим образом: 1-2-3-4-5-6-7-1, 1-3-6-2-5-7-4-1, 1-5-3-7-2-4-6-1.