МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 11. Комбинаторика (26.02.05)

1.

а)

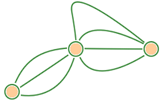Из деревни Филимоново в деревню Ксенофонтово ведут три дороги, а из деревни Ксенофонтово в деревню Оладушкино ведут четыре дороги. Сколько существует путей из деревни Филимоново в деревню Оладушкино?

Ответ Решение

Ответ. 12 путей.

Решение. Нужный нам маршрут имеет вид: Филимоново-Ксенофонтово-Оладушкино. Первый этап этого путешествия Филимоново-Ксенофонтово можно проехать по одной из 3 дорог, т.е. существует 3 способа выбора пути на этом этапе. Когда мы приедем в Ксенофонтово, нам предстоит второй этап путешествия Ксенофонтово — Оладушкино. Этот этап мы можем проехать по одной из 4 дорог, т.е. для каждого из 3-х вариантов выбора пути на первом этапе существует 4 варианта выбора пути на втором. Т.е. всего 3×4=12 вариантов пути.

б)

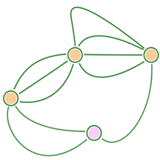От дачного посёлка проложили две дороги до деревни Филимоново и одну дорогу до Оладушкино. Сколько теперь существует путей от Филимоново до Оладушкино?

Ответ Решение

Ответ. 14 путей.

Решение. Теперь существует два маршрута из Филимоново в Оладушкино. Первый вида Филимоново-Ксенофонтово-Оладушкино, а второй — вида Филимоново-дачный посёлок-Оладушкино. По первому маршруту существует 12 вариантов проезда, а по второму маршруту 2 варианта. Т.о. всего 12 + 2=14 вариантов.

2.

В классе 25 школьников. 18 из них на уроках рисуют цветными фломастерами на партах, 10 — делают из бумаги самолётики, а 3 — прилежно занимаются. Сколько учеников этого класса одновременно рисуют и делают самолётики? (Заниматься и при этом рисовать на парте или делать самолётик никто не умеет.)

Ответ Решение

Ответ. 6 учеников.

Решение.
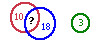
Пусть кружочки обозначают группы учеников, которые рисуют, делают самолётики и прилежно занимаются. Прилежно занимаются трое, значит, на первые две группы остаётся 22 школьника. Так как 18 + 10 больше, чем 22, значит, есть дети, которые относятся и к первой, и ко второй группе. Если бы первый и второй кружочки не пересекались, то при сложении количества детей в первой и во второй группе мы бы получили количество детей в обеих группах. Но так как кружочки пересекаются, то дети, которые и рисуют на партах, и делают самолётики, при сложении 18 и 10 будут посчитаны дважды. Поскольку 18 + 10=22 + 6, то дважды оказались посчитаны 6 детей.

3.

Люся хочет послать Вите записку. У неё есть бумага в клеточку, в линеечку и в кружочек. В записке она может написать одну из трёх фраз: «Люблю», «Целую» и «Поздравляю с 23 февраля». Сколько различных записок может послать Люся?

Ответ Решение

Ответ. 9 записок.

Решение. Люся может выбрать один из трёх видов бумаги для записки и на каждом виде бумаги написать одну из трёх фраз. Т.е. всего 3×3=9 способов написать записку.

4.

Число девочек, решивших задачу, оказалось равно числу мальчиков, не решивших задачу. Кого больше в этом классе: мальчиков или людей, решивших задачу?

Ответ Решение

Ответ. Их поровну.

Решение. Обозначим число девочек, решивших задачу, буквами ДР, число девочек, не решивших задачу, буквами ДН, число мальчиков, решивших задачу — МР, и МН — число мальчиков, не решивших задачу. Из условия следует, что ДР = МН. Спрашивается, что больше: МР + МН или ДР + МР? Очевидно, что эти два выражения равны.

5.

В магазине продают 5 видов чашек, 4 вида блюдец и 2 вида ложек. Сколькими способами можно купить

а)

набор из чашки, блюдца и ложки;

Ответ Решение

Ответ. 40 способов.

Решение. Чашку мы можем выбрать одним из 5 способов, блюдце — одним из 4 способов, ложку — одним из 2 способов. Всего 5×4×2=40 способов сделать покупку.

б)

два предмета с разными названиями?

Ответ Решение

Ответ. 38 способов.

Решение. Существует три вида покупок: чашка-блюдце, блюдце-ложка и ложка-чашка. Существует 5×4=20 покупок первого вида, 4×2=8 покупок второго вида и 2×5=10 покупок третьего вида. Тогда всего 20 + 8 + 10=38 способов сделать покупку.

6.

В лесу растут 362 ёлки. Докажите, что среди них найдутся либо 20 ёлок разной высоты, либо 20 ёлок одинаковой высоты.

Доказательство

Доказательство. Повесим на каждую ёлку табличку, на которой указана её высота. Рассмотрим два случая.
Первый случай. Если получилось так, что существует не менее 20 попарно различных табличек, то всё хорошо: рассмотрим любые 20 табличек и возьмём по одной ёлке с каждым из этих видов табличек — мы нашли 20 ёлок разной высоты.
Второй случай. Если всего существует не более 19 видов табличек, то ёлок хотя бы с одним из этих видов табличек минимум 20, т.к. иначе всего не более, чем 19×19=361 ёлки (не более 19 видов и не более 19 ёлок каждого из них). Но это противоречит условию, т.к. всего ёлок 362. Значит, в этом случае мы нашли 20 ёлок одинаковой высоты.

7.

Меню школьной столовой не меняется и состоит из 10 блюд. Для разнообразия Витя хочет каждый день заказывать такой набор блюд, который он ещё ни разу не заказывал (при этом число блюд не важно — он может заказать все 10 блюд, а может заказать только одно или вовсе ни одного). Сколько дней он сможет так питаться?

Ответ Решение

Ответ. 1024 дня.

Решение. Допустим, что в школьной столовой Вите каждый день дают меню со списком блюд, и он галочками отмечает, какие блюда он сегодня заказывает. Посмотрим, сколько различных вариантов расстановки галочек может быть. Напротив первого блюда он может поставить галочку либо не поставить — два варианта. Для каждого из этих вариантов он может либо поставить галочку напротив второго блюда, либо не ставить. Для каждого из этих 2×2 вариантов он может либо поставить галочку напротив третьего блюда, либо не ставить. Для каждого из этих 2×2×2 вариантов он может либо поставить галочку напротив четвёртого блюда, либо не ставить. И так далее. Таким образом, всего есть 2¹⁰ вариантов расстановки галочек, а значит, 2¹⁰ дней он сможет так питаться.