МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 7. Раскраски (4.12.2004)

Я раскрашу целый свет в самый мой любимый цвет!

1.

Витя и Женя играют в такую игру. У них есть клетчатая таблица 11×11. Каждым ходом они закрашивают любую еще не закрашенную клетку таблицы. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре?

Ответ Решение

Ответ. Выигрывает первый игрок

Решение. После каждого хода любого из игроков количество не закрашенных клеток уменьшается на одну. Вся доска состоит из 121 клетки. А так как в начале они все не закрашены, и всего их нечётное число, то выиграет тот, кто ходит первым.

2

Каждая точка на прямой покрашена либо в красный, либо в синий цвет. Докажите, что можно выбрать три точки одного цвета так, что одна из них лежит ровно посередине между двумя другими.

Решение

Решение. Возьмём две точки одного цвета A и B (допустим, синего). Будем считать, что AB = 1. Если справа от B или слева от А на расстоянии 1 — синяя точка, то задача решена (мы нашли три синие точки на расстоянии 1). В противном случае обе эти точки (обозначим их C и D) — красные.
Поскольку CD = 3, в случае, если слева от C или справа от D на расстоянии 3 — красная точка, задача решена (мы нашли три красные точки на расстоянии 3). В противном случае обе эти точки (обозначим их E и F) — синие.
Если на единицу вправо от E находится синяя точка (обозначим её G), то точки G, B и F — искомые. Пусть точка G — красная.
Если середина отрезка GC (обозначим её H) — красная, то точки G, H, C — искомые. Если точка H — синяя, то искомыми точками будут E, H, A.

3.

Можно ли таблицу 8×8 c вырезанной угловой клеткой разрезать на полоски 1×3?

Ответ

Ответ. Да, можно. Для решения достаточно построить пример.

4.

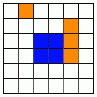Клетки квадрата 6×6 покрашены в синий, белый и оранжевый цвет. Разрежьте квадрат на четыре одинаковые по форме части так, чтобы в каждой части было одинаковое количество клеток каждого цвета.

Решение

Решение.

5.

У Жени есть 6 разных красок. Он хочет раскрасить грани кубика в разные цвета. Сколько различных кубиков он таким образом может получить?

Ответ

Ответ. 30.

6.

Пятнадцать хулиганов вышли на демонстрацию с шариками и построились в колонну 3×5. По команде каждый проткнул иголкой шарик своего соседа. Докажите, что хотя бы один шарик при этом остался целым.

Решение

Решение. Раскрасим места, на которых стоят хулиганы, в шахматном порядке. Тогда каждый хулиган, стоявший на белом месте, проткнул шарик другого хулигана, но который стоял на чёрном месте. И наоборот, любой хулиган, стоявший на чёрном месте, проткнул шарик хулигана, находившегося на белом месте. Но чёрных мест 8, а белых — 7. Значит, «чёрных» шариков могло быть проткнуто не более 7. Тогда хотя бы один такой шарик останется целым.

7.

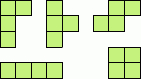Можно ли из пяти фигур, изображённых на рисунке, сложить прямоугольник 4×5?

8.

Каждую грань кубика можно покрасить либо в чёрный, либо в белый цвет. Сколько различных кубиков можно изготовить?