МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 8. С Новым Годом! (11.12.2004)

1.

Можно ли, имея лишь два ведра ёмкостью 6 л и 10 л, набрать 8 л снега?

Ответ Решение

Ответ. Можно.

Решение. Это можно сделать, например, так:

№	6л ведро	10л ведро	Насыпаем
1	0	0	в 10л
2	0	10	из 10л в 6л
3	6	4	из 6л в снег
4	0	4	из 10л в 6л
5	4	0	в 10л
6	4	10	из 10л в 6л
7	6	8

Получаем 8 литров снега в большом ведре.

2.

От старой ёлочной гирлянды осталось пять кусочков, каждый из которых состоит из сцепленных между собой трёх колец. Можно ли, разъединив всего три кольца, составить новую гирлянду из пятнадцати колец?

Ответ Решение

Ответ. Можно.

Решение. Разъединим три кольца, составляющих одно из звеньев. С их помощью можно соединить оставшиеся четыре целых звена в одну гирлянду.

3.

Можно ли заменить звёздочки в равенстве 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 = 0 на знаки + или − так, чтобы равенство стало верным?

Ответ Решение

Ответ. Можно.

Решение. Например, так: 1 – 2 – 3 + 4 + 5 – 6 – 7 + 8 = 0.

4.

Петя пошел гулять с друзьями в десять часов утра. Сначала он катался на санках, потом лепил снеговика, затем играл в снежки, затем валялся в снегу. В половине шестого он вспомнил, что мама велела ему прийти домой пообедать, и пошел домой. На каждое из развлечений, кроме первого, у Пети ушло вдвое меньше времени, чем на предыдущее. Сколько времени Петя катался на санках?

Ответ Решение

Ответ. 4 часа.

Решение. Пусть Петя валялся в снегу t часов. Так как на каждое следующее развлечение он тратил времени в два раза меньше, чем на предыдущее, то тогда он играл в снежки 2t часов, лепил снеговика 4t часов и катался на санках 8t часов. Тогда всё это продолжалось 15t часов. Но с другой стороны Петя гулял с 10 до половины шестого, то есть 7 с половиной часов. Значит, 15t=7,5. Тогда t=0,5 и 8t=4. То есть, Петя катался на санках 4 часа.

5.

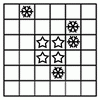Разрежьте фигуру, изображённую на рисунке, на четыре одинаковые по форме части так, чтобы в каждой части содержалось по одной снежинке и одной звёздочке.

Решение

Решение.

6.

В коробке лежит сто звёздочек. Петя и Женя по очереди берут звёздочки из коробки и украшают ими ёлку. За один раз можно взять сколько угодно звёздочек, лишь бы поместилось в руках. Кто возьмёт последнюю звёздочку, тот выиграл. У Жени в руках помещается 20 звёздочек, а у Пети — десять. Может ли Петя выиграть у старшего брата?

Ответ Решение

Ответ. Нет.

Решение. Покажем, что существует стратегия, следуя которой Женя может обеспечить себе победу, вне зависимости от того, каким он будет ходить: первым или вторым.
Сколько бы Петя не взял звёздочек, Женя всегда может взять столько звёздочек, чтобы в сумме получилось 20. Если Женя ходит вторым, то после первого хода Жени в коробке останется 80 звёздочек, после второго — 60, после третьего — 40, после четвёртого — 20. Дальше Петя делает свой ход: берёт сколько-то звёздочек, но все забрать не может. А после этого Женя забирает все оставшиеся и выигрывает.
Если же Женя ходит первым, то самым первым ходом он забирает 20 звёздочек, а дальше, как и в первом случае, дополняет количество Петиных звёздочек до двадцати.

7.

Можно ли заменить звёздочки в равенстве 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 = 0 на знаки + или − так, чтобы равенство стало верным?