МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 10. Просто задачи (19.02.2004)

1.

Арбуз разрезали на четыре части и съели. Получилось пять корок. Могло ли такое быть?

Ответ Решение

Ответ. Да.

Решение. Вырезали цилиндрический кусочек с двумя корочками, а оставшееся разрезали на три части.

2.

Как при помощи только пяти цифр 5, знаков арифметических действий и скобок представить каждое из чисел от 0 до 10 включительно?

Решение

Решение.
5·(55 − 55)=0
5·(5 − 5) + 5:5=1
(5 + 5):5 + 5 − 5=2
5:5 + (5 + 5):5=3
(5 + 5 + 5 + 5):5=4
5 − 5 + 5 − 5 + 5=5
5 + 55:55=6
(5·5 + 5 + 5):5=7
(5 + 5 + 5):5 + 5=8
(5·5 − 5):5 + 5=9
(5·5 + 5·5):5=10

3.

У старухи Шапокляк есть ковёр 4×4 метра. Моль проела в нём 15 дырок (каждая дыра — точкa). Может ли старуха Шапокляк вырезать из ковра маленький целый коврик размером 1×1 метр?

Решение

Решение. Разобьём ковёр на 16 квадратов размером 1×1 метр. Так как дырок всего 15, хотя бы один квадрат окажется без дырок. Его можно вырезать из ковра.

4.

В классе школьники сидят по одному человеку за партой — в три ряда по пять человек. Каждый школьник подарил своему соседу (справа, слева, впереди или сзади сидящему) по конфете. Докажите, что есть школьник, которому подарили по крайне мере две конфеты.

Решение

Решение. Раскрасим парты в шахматном порядке в чёрный и белый цвет. Заметим, что каждый школьник подарил конфету сидящему за партой противоположного цвета. Поскольку парт одного цвета (допустим, белых) —восемь, а парт другого цвета (чёрных) — семь, школьникам, сидящим за чёрными партами, подарят восемь конфет на семерых. Значит, кому-то достанется по крайней мере две конфеты.

5.

Каждая клетка доски размером 100×100 покрашена в один из 99 цветов. Если в какой-то строке или каком-то столбце есть две клетки одного цвета, то разрешается перекрасить в этот цвет все остальные клетки этой строки (столбца). Всегда ли можно с помощью таких операций перекрасить всю доску в один цвет?

Ответ Решение

Ответ. Да, всегда.

Решение. Возьмём любую строку. Так как цветов 99, а клеток в строке — 100, есть по крайней мере две клетки одного цвета. Значит, мы можем перекрасить всю строку в этот цвет. Воспользуемся этим и покрасим каждую строку в какой-нибудь цвет.
Теперь у нас есть 100 строк, покрашенные в 99 цветов. Значит, по крайней мере две строки покрашены в один цвет (допустим, красный). То есть в любом столбце есть две красные клетки. Покрасим все столбцы в красный цвет.

6.

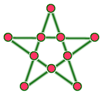
В деревне Маломехматово 10 домов и пять прямолинейных улиц, причём на каждой улице находится 4 дома. Нарисуйте схему расположения домов в деревне.

Решение

Решение.