МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 6. Игры со спичками (27.11.2004)

Спички детям не игрушка!

1.

Как из пяти спичек, не ломая их, сделать восемь?

2.

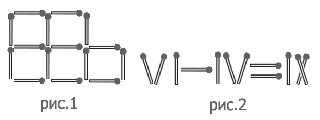
Спички расположены так, как показано на рисунке 1. Снимите три спички, чтобы получились три одинаковых квадрата.

3.

На рис. 2 из спичек выложено неверное равенство. Переложив 1 спичку, превратите равенство в верное.

4.

Из 10 спичек составьте три квадрата. Попробуйте это сделать двумя способами.

5.

В трёх кучках лежат спички, по 10 спичек в каждой. Играют Аня и Вова. Ход состоит в том, что игрок забирает несколько спичек, но только из какой-либо одной кучки. Начинает Аня. Побеждает тот, кому достанется последняя спичка. Может ли кто-нибудь из игроков играть так, чтобы наверняка выиграть, как бы ни старался другой?

Ответ Решение

Ответ. Аня может выиграть.

Решение. Аня может забрать целиком одну кучку, а затем повторять ходы Вовы. Тогда после каждого Аниного хода в двух кучках остаётся равное количество спичек, а после каждого Вовиного хода равенство нарушается. Поэтому выиграет Аня.

6.

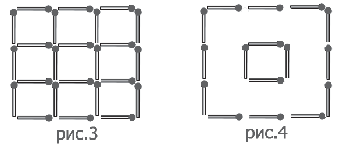
На рисунке 3 из спичек сложен квадрат 3×3. Уберите

а)

4 спички, чтобы осталось 5 квадратов;

б)

8 спичек, чтобы осталось 2 квадрата;

в)

6 спичек, чтобы осталось 3 квадрата.

7.

Из шестнадцати спичек выложен «план крепости», окруженной глубоким рвом (рис. 4). Как при помощи двух досок-спичек, длина которых равняется ширине рва, пробраться в крепость?

8.

Из шести спичек сложите четыре треугольника.

9.

У Ани и Вовы есть 20 спичек. За один ход разрешается взять одну, две или три спички. Начинает Аня. Проигрывает тот, кому нечего взять. Кто выигрывает при правильной игре?