МАЛЫЙ МЕХМАТ МГУ

Кружок 7 класса
Руководители Сергей Александрович Дориченко и Степан Львович Кузнецов
2008/2009 учебный год
2008/2009 учебный год
Занятие 11
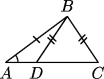
- 1.
-
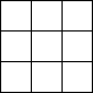
Сколько квадратов
- а)
- изображено на рис. 1?
Ответ. 14.- б)
- можно изобразить с вершинами в точках на рис. 2?
Ответ. 20.
 |
 |
| Рис. 1 | Рис. 2 |
- 2.
-
Шахматный конь ходит по диагонали прямоугольника 2×3
(или, что то же, 3×2). Может ли
он обойти все поля доски 3×3, побывав на каждом поле по
одному разу?
Ответ. Нет.Решение. На центральное поле конь не может попасть ни с одного другого поля.
- 3.
-
У квадрата n×n закрасили
все клетки по периметру. При каких n закрашенных клеток меньше,
чем незакрашенных?
Ответ. При n > 6.Решение. Прямой подсчёт показывает, что n = 1, 2, 3, 4, 5, 6 не подходят. При n ≥ 7 число неокрашенных клеток не меньше 5(n − 2), а окрашенных клеток всего 4(n − 1). Поскольку 4(n − 1) < 5(n − 2) (т. к. n > 6), при n ≥ 7 окрашенных клеток больше, чем неокрашенных.
- 4.
-
Какие общие делители есть у чисел
а) 2009 и 2010; б) 2009 и 2011?
Ответ. а) 1. б) 1.Указание. Любой общий делитель двух чисел делит их разность.
- 5.
-
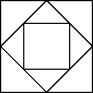 Рис. 3
Рис. 3- а)
- Найдите отношение площадей самого большого и самого маленького квадратов на рис. 3.
- б)
- Что можно сказать про площадь самого среднего квадрата на том же рисунке?
Ответ. Площади маленького, среднего и большого квадратов относятся как 1 : 2 : 4.Решение.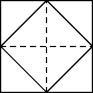 Квадрат, вершины которого являются серединами сторон другого
квадрата, в два раза меньше того по площади. Это видно из
рисунка, на котором квадраты разрезаны на равные треугольники.
Значит, средний квадрат вдвое меньше большого, а самый маленький
вдвое меньше среднего.
Квадрат, вершины которого являются серединами сторон другого
квадрата, в два раза меньше того по площади. Это видно из
рисунка, на котором квадраты разрезаны на равные треугольники.
Значит, средний квадрат вдвое меньше большого, а самый маленький
вдвое меньше среднего.
- 6.
-
Семиклассник Сёма придумал новый
признак равенства треугольников: если две стороны и угол не
между ними одного треугольника соответственно равны двум сторонам и
углу не между ними другого треугольника, то такие
треугольники равны. Прав ли Сёма?
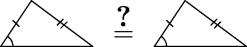 Ответ. Нет.
Ответ. Нет. - 7.
-
На окружности с центром O последовательно отмечают точки A1, A2, A3, ... (первые несколько можно увидеть на рис. 4) так, что ∠A1OA2 = ∠A2OA3 = ... = 19°.
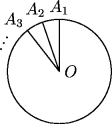 Рис. 4
Рис. 4- а)
- Чему равен ∠A1OA20?
- б)
- Какая точка первой попадёт в число уже отмеченных?
Ответ. а) 1°. б) A361.Решение. а) 19² = 361.
б) Из пункта а) мы знаем, что после 19 шагов (поворотов на 19°) точка смещается относительно исходной на 1°. Кроме того, если точка попадёт в уже отмеченную, то после этого новых точек не появится: все последующие точки будут попадать в уже отмеченные. Значит, совпадение произойдёт в точности тогда, когда будут отмечены все точки B, такие что ∠A1OB выражается целым числом градусов. Всего таких точек 360, поэтому первой точкой, уже отмеченной ранее, будет 361-я точка A361.
Дополнительные задачи
- 8.
-
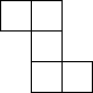 Разрежьте фигуру, изображённую на рисунке, на части, из
которых можно сложить квадрат.
Разрежьте фигуру, изображённую на рисунке, на части, из
которых можно сложить квадрат.
- 9.
- Дан угол величиной 7°. С помощью циркуля и линейки постройте угол величиной 1°.
- 10.
- Из пункта A в пункт B вышел пешеход и одновременно с ним из B в A выехал мотоциклист. Встретив пешехода, мотоциклист развернулся, довёз пешехода до пункта B, а затем добрался до пункта A. Во сколько раз в результате непредусмотренных разъездов мотоциклист проиграл во времени, если пешеход, наоборот, выиграл во времени в 4 раза?