МАЛЫЙ МЕХМАТ МГУ

Кружок для старшеклассников, не участвовавших ранее в математических кружках

Занятие 22 (4 апреля 2015 года). Конструкции

1.

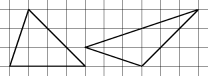Разрежьте первый треугольник на части, из которых можно сложить второй (смотрите рисунок).

2.

Альпинист стоит на вершине отвесной скалы высотой 100 м с уступом на высоте 50 м. У него есть 77-метровая верёвка и нож. На вершине скалы и на уступе вбиты колышки, к которым можно привязать верёвку. Как альпинисту спуститься со скалы (разумеется, не прыгая)?

3.

Нарисуйте ломаную, состоящую из четырех отрезков, которая проходила бы через все девять точек в узлах решётки 2×2.

4.

Верно ли, что если все грани многогранника — квадраты, то этот многогранник — куб?

5.

Отметьте на доске 8×8 несколько клеток так, чтобы любая (в том числе и любая отмеченная) клетка граничила по стороне ровно с одной отмеченной клеткой.

6.

На доске записаны числа 1, 2¹, 2², 2³, 2⁴, 2⁵. Разрешается стереть любые два числа и вместо них записать их разность – неотрицательное число. Может ли на доске в результате нескольких таких операций остаться только число 15?

7.

Найдите какие-нибудь четыре попарно различных натуральных числа a, b, c, d, для которых числа a² + 2cd + b² и c² + 2ab + d² являются полными квадратами.

8.

Существуют ли такие натуральные числа a, b, c, что a³ + b² + c²=2¹⁰⁰?

9.

Барон Мюнхгаузен утверждает, что может нарисовать такой многоугольник и точку внутри него, что ни одна из сторон многоугольника не будет видна из неё целиком. Не ошибается ли он? (Многоугольником называется замкнутая ломаная без самопересечений).

10.

Дан угол величиной 7°. С помощью циркуля и линейки постройте угол в 1°.

11.

На шахматной доске расставлены фигуры так, что на каждой горизонтали и вертикали стоит не меньше двух фигур. Всегда ли можно снять с доски несколько фигур так, чтобы на каждой горизонтали и вертикали осталось ровно по одной фигуре?