МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 9. Геометрия

1.

Внутренние покои дворца султана Ибрагима ибн Саида состоят из ста одинаковых квадратных комнат, расположенных в виде квадрата 10×10. Если у двух комнат есть общая стена, то в ней обязательно есть ровно одна дверь. А если стена внешняя, то в ней обязательно есть ровно одно окно. Сколько окон и дверей в покоях Ибрагима ибн Саида?

Ответ Решение

Ответ. 40 окон, 180 дверей.

Решение. Поскольку во дворце султана 4 наружных стены, по длине каждой из которых располагаются 10 комнат, и 18 внутренних перегородок (9 продольных и 9 поперечных), каждая также длиной 10 комнат, можно определить число окон (10·4 = 40) и дверей (10·18 = 180). 

2.

У двух человек было по квадратному торту. Каждый сделал на своём торте по два прямолинейных разреза от края до края. При этом у одного получилось три куска, а у другого — четыре. Как такое могло быть?

Ответ

Ответ. Это могло получиться, если в первом случае разрезы не пересекались, а во втором — пересеклись. Например, если в первом случае они были параллельны друг другу, а во втором — перпендикулярны.

3.

Есть три одинаковых кирпича и линейка. Как без вычислений узнать длину главной диагонали кирпича? (Главная диагональ — та, которая соединяет две противоположные вершины кирпича. Она лежит внутри кирпича и снаружи не видна.)

Ответ

Ответ. Например, сначала положить один за другим три кирпича, а затем убрать тот, который лежит посередине, и измерить расстояние между соответствующими вершинами двух оставшихся кирпичей.

4.

Студенты кафедры высшей геометрии и топологии, находясь летом на отдыхе, разрезали арбуз на четыре части и съели. Могло ли после этого остаться пять корок?

Ответ Решение

Ответ. Могло.

Решение. Если постараться, из арбуза можно вырезать кусок в виде столбика, идущего сквозь весь арбуз. У этого куска будут две корки, соединенные арбузной мякотью. Когда его съедят, останется две корки. А оставшуюся часть арбуза можно как угодно разрезать на три части, от них останется ещё три корки.

5.

У Джузеппе есть лист фанеры, размером 22×15. Джузеппе хочет вырезать из него 22 прямоугольных заготовки размером 3×5. Как ему это сделать?

Ответ Решение

Ответ.

Решение. Прежде всего, заметим, что Джузеппе не сможет получить заготовок больше, чем (22 · 15) : (3 · 5) = 22 штуки. Теперь приступим к разрезанию. Разрежем наш лист на три поперёк стороны 22: 5×15, 5×15 и 12×15. Теперь третий кусок разрежем вдоль стороны длиной 12 на четыре равных куска 3×15. Всего получится 6 кусков — два 5×15 и четыре 3×15. Из первых двух кусков мы получим по 5 заготовок 5×3, а из оставшихся четырех — по 3 заготовки 3×5. Итого получится 22 куска (см. рисунок в ответе).

6.

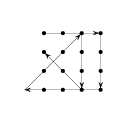
Как, не отрывая карандаша от бумаги, провести шесть отрезков таким образом, чтобы полученная ломаная прошла через 16 точек, расположенных в узлах квадратной сетки 4×4?

Ответ

Ответ.

7.

Ковер-самолет летает только тогда, когда имеет прямоугольную форму. У Ивана-царевича был ковер-самолет размером 9×12. Как-то раз Змей Горыныч подкрался и отрезал от этого ковра маленький коврик размером 1×8. Иван-царевич очень расстроился и хотел было отрезать еще кусочек 1×4, чтобы по-лучился прямоугольник 8×12. Но Василиса Премудрая предложила поступить по-другому. Она разрезала ковер на три части, из которых волшебными нитками сшила квадратный ковер-самолет размером 10×10. Сможете ли Вы догадаться, как Василиса Премудрая переделала испорченный ковер?

Решение

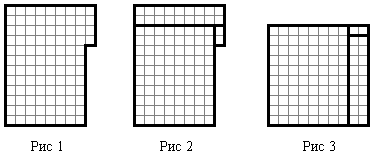
Решение. После того как Змей Горыныч испортил ковер, Иван-царевич мог отрезать от этого ковра кусочек размером 1×4 и превратить его в ковер размером 8×12. Это значит, что после ухода Змея Горыныча ковер выглядел так, как показано на рис. 1. Василиса Премудрая разрезала этот ковер так, как показано на рис. 2, и сшила так, как показано на рис. 3.

8.

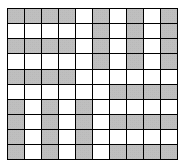
Можно ли в квадрате 10×10 расставить 12 кораблей 1×4 (для игры типа «морского боя») так, чтобы корабли не соприкасались друг с другом (даже вершинами)?

Ответ Решение

Ответ. Можно.

Решение.

9.

В круге отметили точку. Разрежьте круг

а)

на три;

б)

на две части так, чтобы из них можно было составить новый круг, у которого отмеченная точка будет в центре.

Решение

Решение.

a) Нужно вырезать из круга два маленьких равных кружка — один с центром в центре круга, а другой с центром в отмеченной точке, и затем поменять эти кружки местами.

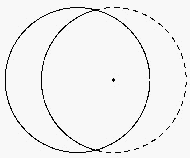
б) Линия разреза — дуга того же радиуса, что и у данного круга, с центром в отмеченной точке (см. рис.).

10.

На бумаге нарисован квадрат и невидимыми чернилами нанесена точка P. Человек в специальных очках видит точку. Если провести прямую, то он отвечает на вопрос, по какую сторону от неё лежит точка P (если точка лежит на прямой, то он говорит, что P лежит на прямой).

а)

Как за четыре вопроса узнать, лежит ли точка Р внутри квадрата?

б)

Удастся ли это сделать за три вопроса?

Ответ Решение

Ответ. б) Удастся.

Решение.

а) Проведём прямую, содержащую одну из сторон квадрата. Если точка лежит по другую сторону от этой прямой, чем квадрат, то она точно не лежит в квадрате. Иначе проведём прямую, содержащую вторую сторону квадрата и проведём аналогичные рассуждения. Проведя все четыре прямые, содержащие стороны квадрата, мы узнаем, лежит ли точка внутри квадрата.

б) Проведём сначала две прямые, содержащие диагонали квадрата. Они разобьют лист бумаги на четыре части. По ответам на первые два вопроса мы узнаем, в какой из этих частей лежит точка. Теперь проведём прямую, содержащую ту сторону квадрата, которая лежит в той же части плоскости, что и точка. Эта прямая разобьёт указанную часть плоскости ещё на две части, одна из которых будет внутри квадрата, а другая — снаружи. По ответу на третий вопрос мы узнаем, лежит ли точка внутри квадрата. Обратите внимание: теперь мы знаем не только то, лежит ли точка внутри квадрата, но и то, в какой из четырёх частей квадрата (на которые его делят диагонали) она лежит.

В этом решении ничего не сказано о случаях, когда точка оказывается на одной или нескольких из прямых, которые мы проводим. Разберите эти случаи самостоятельно.