МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 22. Оценка плюс пример

1.

Какое наибольшее число трёхклеточных уголков можно вырезать из клетчатого квадрата 8×8?

Ответ Решение

Ответ. 21.

Решение. Оценка: 64 = 3·21 + 1. Поэтому больше 21 уголка из квадрата 8×8 вырезать не удастся просто по соображениям площади.
Пример: на рисунке ниже показано, как вырезать ровно 21 уголок из доски 8×8.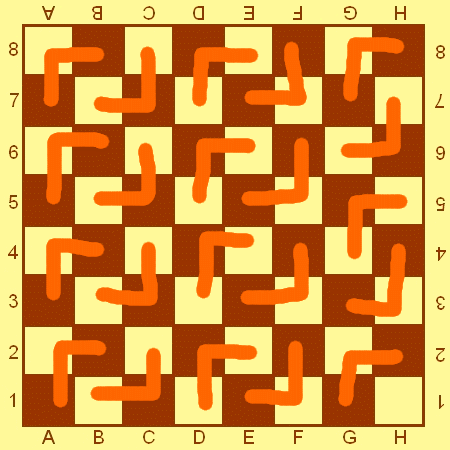

2.

а)

8 кузнецов должны подковать 10 лошадей. Каждый кузнец тратит на одну подкову 5 минут. Какое наименьшее время они должны потратить на работу? (Учтите, лошадь не может стоять на двух ногах.)

б)

А если кузнецов 48, а лошадей 60?

Ответ Решение

Ответ. 25 минут в обоих случаях.

Решение.

Оценка. 10 лошадей — это 40 копыт. Если кузнецы выполняют одинаковый объём работы (по-другому работать невыгодно, так как производительность у всех одинаковая), то каждый должен подковать 40 : 8 = 5 копыт, потратив на это 5·5 = 25 минут (в случае, если им всем удастся работать одновременно так, чтобы никакая лошадь не стояла на двух ногах). Так же делается оценка в пункте б.

Пример. Разобьём кузнецов на группы по 4, а лошадей — на группы по 5. В пункте а таких групп будет по две, а в пункте б — по 12. Каждая группа кузнецов будет работать со своей группой лошадей по следующему графику:

Время	I кузнец	II кузнец	III кузнец	IV кузнец
1-5 минуты	1	2	3	4
6-10 минуты	2	3	4	5
11-15 минуты	3	4	5	1
16-20 минуты	4	5	1	2
21-25 минуты	5	1	2	3

В этой таблице указан номер лошади, которую в соотвествующий момент времени подковывает кузнец. В каждой строке все лошади разные, значит, никакой лошади не нужно стоять на двух ногах. Каждый номер от 1 до 5 встречается в таблице 4 раза, значит, каждой лошади подковали все 4 ноги.

3.

Найдите наименьшее натуральное число:

а)

кратное 10, сумма цифр которого равна 10;

б)

кратное 100, сумма цифр которого равна 100;

в)

кратное 5, сумма цифр которого равна 25.

Ответ Решение

Ответ. а) 190; б) 19999999999900; в) 2995.

Решение.

а) Чтобы число делилось на 10, оно должно оканчиваться на 0. Если число будет двузначным с нулём на конце, то его сумма цифр будет не больше 9. Значит, число должно быть по крайней мере трёхзначным. Наименьшим из трёхзначных чисел с указанными свойствами будет то, у которого в разряде сотен стоит единица. Чтобы сумма цифр этого числа была равна 10, в разряде десятков у него должна стоять девятка.

б) Чтобы число делилось на 100, оно должно оканчиваться двумя нулями. Если число будет не более чем 13-значным с двумя нулями на конце, то (поскольку каждая цифра не больше 9) сумма его цифр будет не больше 99. Значит, число должно быть по крайней мере 14-значным. Из 14-значных чисел с указанными свойствами наименьшим числом будет то, у которого в старшем разряде единица. Тогда остальные его цифры (кроме двух нулей на конце) должны быть девятками, и это будет число 19999999999900.

в) Чтобы число делилось на 5, оно должно оканчиваться нулём или пятёркой. Если число не более чем трёхзначное и оканчивается нулём или пятёркой, то сумма его цифр не больше 5+9+9 = 23. Значит, число должно быть по крайней мере четырёхзначным. Среди четырёхзначных чисел с указанными свойствами наименьшим будет то, у которого в разряде тысяч стоит наименьшая цифра. Если там стоит единица, то сумма цифр числа не превосходит 1+9+9+5 = 24. Значит, там должна стоять хотя бы двойка. В последнем случае сумма цифр 25 достижима, только если это число 2995. Остальные числа с указанными свойствами будут больше найденного.

4.

Какое наименьшее число клеточек на доске 8×8 можно закрасить в чёрный цвет так, чтобы была хотя бы одна закрашенная клетка:

а)

в любом квадратике 2×2?

б)

в любом уголке из трёх клеточек?

Ответ Решение

Ответ. а) 16; б) 32.

Решение.

Оценка. Разобъём наш квадрат на 16 квадратиков 2×2. В пункте а в каждом из них должна быть хотя бы одна закрашенная клетка (иначе будет квадратик без закрашенных клеток), так что клеток не меньше 16. В пункте б в каждом из этих квадратиков должно быть хотя бы две закрашенные клетки, иначе в этом квадратике поместится незакрашенный уголок. Поэтому в пункте б нужно закрасить

Пример. В пункте а закрасим на доске клетки A1, A3, A5, A7, C1, C3, C5, C7, E1, E3, E5, E7, G1, G3, G5, G7 (обозначения клеток — как на шахматной доске). Легко видеть, что закрашено 16 клеток, и при этом в любом квадратике 2×2 есть ровно одна закрашенная клетка. В пункте б можно использовать, например, обычную шахматную раскраску: при этом будет закрашено 32 клетки, а в каждом трёхклеточном уголке будет либо одна белая клетка и две чёрных, либо одна чёрная и две белых.

5.

В пруд пустили 30 щук, которые стали кушать друг друга. Щука считается сытой, если она съела хотя бы трёх щук. Какое наибольшее количество щук могло насытиться, если съеденные сытые щуки при подсчёте тоже учитываются?

Ответ Решение

Ответ. 9.

Решение. Оценка: 10 или больше щук сытыми быть не могут — ведь тогда были бы съедены хотя бы 30 щук, то есть вообще все щуки, чего быть не может.
Пример: на картинке ниже показано, как щукам есть друг друга, чтобы насытилось ровно 9 щук. Зелёными точками отмечены сытые щуки, красными — голодные.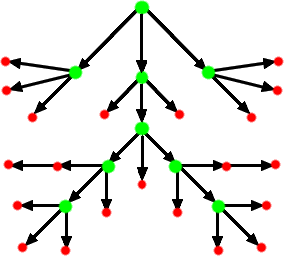

6.

У каждого из 222 шестиклассников на Малом Мехмате не более двух близких приятелей. Оказавшись в одном помещении, два близких приятеля начинают непрерывно болтать, и всякая работа в этом помещении прекращается. Какое наименьшее число аудиторий необходимо иметь Евгению Александровичу, чтобы обеспечить бесперебойную работу всей параллели 6 класса?

Ответ Решение

Ответ. Три аудитории.

Решение.

Оценка: двух аудиторий может не хватить. В самом деле, если среди шестиклассников есть трое попарно знакомых, то их нельзя посадить ни в одну, ни в две аудитории.

Пример: трёх аудиторий всегда хватит. Объясним, как можно рассадить школьников по трем аудиториям. Всех школьников можно разделить на несколько групп так, чтобы школьники из разных групп между собой знакомы не были (может быть, такая группа будет только одна). Тогда эти группы можно рассаживать по аудиториям независимо друг от друга.

Внутри каждой группы возможна только одна из двух ситуаций. Либо первый человек знаком со вторым, второй с третьим, третий с четвёртым, ..., предпоследний с последним, последний с первым. Либо всё то же самое, только первый и последний не знакомы. Другие ситуации невозможны, потому что у каждого школьника не больше двух знакомых. (Некоторые группы могут состоять и всего из одного человека, который ни с кем не знаком.) Во втором случае всю группу можно рассадить в две аудитории (школьников с нечётными номерами — в первую аудиторию, школьников с чётными — во вторую). В первом случае делаем то же самое, а если школьников в группе нечётное число, то последнего придётся посадить в третью аудиторию (он знаком с первым, сидящим в первой аудитории, и с предпоследним, номер которого чётный и который поэтому сидит во второй аудитории).

7.

На старт «Весёлого забега» на 3000 м выходит команда из трёх математиков. Им выдается один одноместный самокат. Дорожка прямая, стартуют все одновременно, а в зачёт идет время последнего пришедшего на финиш. Каково минимальное возможное время прохождения дистанции, если бегают все трое со скоростью 125 м/мин, а на самокате ездят со скоростью 250 м/мин?

Ответ Решение

Ответ. 20 минут.

Решение.

Пример. Первый едет треть пути на самокате, бросает его, бежит дальше пешком. Второй бежит треть пути, хватает валяющийся самокат, берёт его, едет треть пути, бросает, бежит дальше пешком. Третий бежит две трети пути, хватает самокат и финиширует одновременно со сокомандниками. В итоге каждый треть пути (1 км) едет и две трети пути (2 км) бежит. Значит, каждый спортсмен тратит 1000:250 + 2000:125 = 20 минут на преодоление дистанции.

Оценка. Очевидно, что возвращаться назад, чтобы передать транспортное средство товарищу, невыгодно. Поэтому на самокате нужно двигаться только вперёд. Если кто-то проедет на самокате менее трети дистанции, то он потратит на весь забег более 20 минут. Значит, всем нужно проехать ровно треть.

8.

На какое наибольшее количество разных прямоугольников можно разрезать по линиям сетки:

а)

прямоугольник 5×6 клеточек;

б)

прямоугольник 12×6 клеточек;

в)

прямоугольник 2×36 клеточек?

Ответ Решение

Ответ. а) 7; б) 13; в) 12.

Решение.

Оценка. Разные прямоугольники — разные по форме или по площади. Прямоугольников площадью в одну клеточку может быть не более одного, площадью в две и в три клеточки — тоже. А вот в 4 клеточки уже может быть два варианта: прямоугольник 1×4 и квадрат 2×2. Таким образом, прямоугольник площадью 1+2+3+4+4=14 клеток можно разрезать не более чем на 5 различных прямоугольников.

Минимальные площади прямоугольников: 1, 2, 3, 4, 4, 5, 6, 6, 7, 8, 8, 9, 9, ...

Аналогичные рассуждения приводят к ответам: а) Площадь равна 30, можно сделать не более 7 прямоугольников.
б) Площадь равна 72; не более 13 прямоугольников.
в) Площадь 72; но прямоугольник 3—3 не помещается внутри прямоугольника 2×36, поэтому его использовать нельзя; в итоге получаем не более 12 прямоугольников.

Примеры. На рисунках ниже показано, как разрезать прямоугольник 5×6 на 7 прямоугольников, 12×6 на 13 прямоугольников и прямоугольник 2×36 на 12 прямоугольников.