МАЛЫЙ МЕХМАТ МГУ
Кружок 6 класса
Руководитель Евгений Александрович Асташов
2012/2013 учебный год
2012/2013 учебный год
Занятие 20. Раскраски
При решении задач этого занятия вам пригодится уже знакомая вам шахматная раскраска, а также следующие двухцветные и многоцветные раскраски: |
 |
 |
 |
 |
| Раскраска 1 | Раскраска 2 | Раскраска 3 | Раскраска 4 | Раскраска 5 |
- 1.
-
- а)
- Из обычной шахматной доски 8×8 вырезали клетки C5 и G2. Можно ли то, что осталось, замостить доминошками 1×2?
- б)
- Тот же вопрос, если вырезали клетки C6 и G2.
Подсказка. Используйте шахматную раскраску. - 2.
-
Можно ли разбить квадрат 8×8 с отрезанным уголком на прямоугольники 1×3?
Подсказка. Воспользуйтесь раскраской 1.
- 3.
-
Можно ли доску размером 10×10 клеток разрезать на фигурки в форме буквы T из четырёх клеток, как на рисунке ниже?
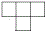Подсказка. Используйте шахматную раскраску. - 4.
-
Можно ли доску 10×10 разрезать на фигурки из четырёх клеток в форме буквы Г, как на рисунке ниже?
Подсказка. Воспользуйтесь раскраской 3. - 5.
- Можно ли квадрат 6×6 разрезать на прямоугольники 1×4? Придумайте раскраску для решения этой задачи самостоятельно.
- 6.
-
Доска 8×8 разрезана на доминошки размером 2×1. Может ли быть 15 вертикальных и 17 горизонтальных доминошек?
Подсказка. Воспользуйтесь раскраской 3.
- 7.
-
Можно ли из квадрата 7×7 вырезать 10 квадратов 2×2?
Подсказка. Воспользуйтесь раскраской 4.
- 8.
-
На клетчатой бумаге произвольным образом отмечено 20 клеток. Докажите, что среди них всегда можно выбрать не менее 5 клеток, попарно не соприкасающихся друг с другом. Соприкасающимися считаются клетки, имеющие хотя бы одну общую вершину.
Подсказка. Воспользуйтесь раскраской 2.
- 9.
-
Из листа клетчатой бумаги размером 17×17 клеточек вырезали 35 квадратиков 2×2 (режут по линиям). Докажите, что из оставшейся части листа можно вырезать ещё хотя бы один такой же квадратик.
Подсказка. Воспользуйтесь раскраской 5.
- 10.
-
В левый нижний угол шахматной доски 8×8 поставлено в форме квадрата 3×3 девять фишек. Фишка может прыгать на свободное поле через рядом стоящую фишку, то есть симметрично отражаться относительно её центра (прыгать можно по вертикали, горизонтали и диагонали). Можно ли за некоторое количество таких ходов поставить все фишки вновь в форме квадрата 3×3, но в другом углу:
- а)
- левом верхнем;
- б)
- правом верхнем?
Подсказка. Воспользуйтесь раскраской 3. - 11.
-
Кусок сыра имеет форму кубика 3×3×3, из которого вырезан центральный кубик. Мышь начинает грызть этот кусок сыра. Сначала она съедает некоторый кубик
1×1×1. После того, как мышь съедает очередной кубик 1×1×1, она приступает к съедению одного из соседних (по грани) кубиков с только что съеденным. Сможет
ли мышь съесть весь кусок сыра?
Подсказка. Используйте шахматную раскраску.
- 12.
-
Треугольник разбит на треугольнички (25 штук), как показано на рисунке. Жук может ходить по треугольнику, переходя между соседними (по стороне) треугольничками. Какое максимальное количество треугольничков может пройти жук, если в каждом он побывал не больше одного раза?
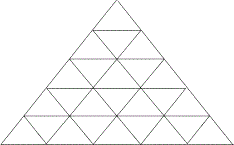Подсказка. Используйте шахматную раскраску.