МАЛЫЙ МЕХМАТ МГУ

Кружок 6 класса

Занятие 14. География и путешествия

1.

Известно, что любую политическую карту можно покрасить в четыре цвета правильно, то есть так, чтобы любые две соседние страны были покрашены в разные цвета. Докажите, что для этого может не хватить трёх цветов. (Нарисуйте какую-нибудь политическую карту, которую нельзя правильно покрасить в три цвета.)

Решение

Решение. На рисунке приведён пример такой карты. Ясно, что в какой бы цвет мы ни покрасили первую страну, остальные страны красить в тот же цвет будет уже нельзя. Значит, их можно будет красить только в один из двух оставшихся цветов. А тогда две из них обязательно окажутся одного цвета.

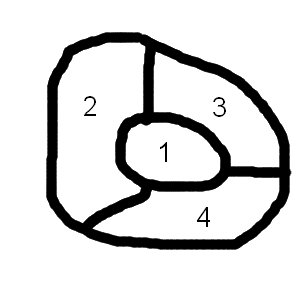
2.

На каникулах Варя летала в Душанбе. Рейс 505 «Аэрофлота» вылетает из Москвы в 12:00, а прилетает в Душанбе в 18:00 (по местному времени). Обратный рейс 506 вылетает в 8:00, а прилетает в 12:00 (по местному времени).

а)

Какая разница во времени между Москвой и Душанбе?

б)

Сколько времени каждый раз длился перелёт Вари?

Ответ Решение

Ответ. а) 1 час; б) 5 часов.

Решение. «Продолжительность» полёта Вари из Москвы в Душанбе равна 6 часам, а полёта обратно — 4 часам. Разница в «продолжительности» полёта Вари туда и обратно составляет два часа. В одном случае разница во времени добавляется ко времени полёта, в другом — вычитается из него. Так что разница во времени составляет 1 час, а время полёта 5 часов.

3.

В некотором государстве из каждого города выходит по три дороги.

а)

Может ли в этом государстве быть ровно 100 дорог?

б)

Сколько в этом государстве дорог, если в нём 100 городов?

Ответ Решение

Ответ. а) Нет; б) 150.

Решение.

а) Если в этой стране n городов, то дорог в ней будет 3 · n : 2. (Из каждого из n городов выходит по три дороги, но каждую дорогу мы считаем дважды.) Поэтому число дорог должно делиться на 3. Или так: если дорог 100, каждая дорога соединяет два города, и из каждого города выходит по три дороги, то городов должно быть 100 · 2 : 3, а это нецелое число.

б) Пользуясь рассуждениями пункта а для n = 100, получим, что число дорог в государстве равно 3 · 100 : 2 = 150.

4.

На железнодорожной платформе с утра собралось много народу в ожидании электрички. На первой электричке уехала десятая часть всех ожидавших, на второй — седьмая часть оставшихся, а на третьей — пятая часть оставшихся.

а)

Сколько пассажиров было на платформе первоначально, если после отхода третьей электрички там осталось 216 пассажиров?

б)

Какое наименьшее ненулевое количество пассажиров могло остаться на платформе после отхода третьей электрички при этих условиях?

Ответ Решение

Ответ. а) 350; б) 216.

Решение.

а) Решая с конца, получим, что перед отходом третьей электрички на платформе было 216 : 4 · 5 = 270 пассажиров, перед отходом второй — 270 : 6 · 7 = 315 пассажиров, а перед отходом первой — 315 : 9 · 10 = 350 пассажиров.

б) Рассуждая аналогично пункту а, получим, что если после отхода третьей электрички на перроне осталось n пассажиров, то первоначально их там было ((n : 4 · 5) : 6 · 7) : 9 · 10 = n : 216 · 350. Поэтому n должно делиться на 216, и минимально возможное ненулевое значение n равно 216. Обратите внимание, что хотя дробь 350/216 сократима, её здесь нельзя заменить на 175/108 (подумайте почему).

5.

Из города в деревню одновременно вышли два пешехода. Один из них половину затраченного времени шёл со скоростью 5 км/ч, а вторую половину — со скоростью 3 км/ч. Второй же пешеход первую половину пути шёл со скоростью 3 км/ч, а вторую половину — со скоростью 5 км/ч. Кто из пешеходов придёт в деревню раньше?

Ответ Решение

Ответ. Первый.

Решение. Посчитаем средние скорости пешеходов. (Напомним, что средняя скорость — это частное от деления всего пройденного пути на всё время, затраченное на его прохождение.) Пусть расстояние от города до деревни равно S км, и первый пешеход проходит это расстояние за время Т. Тогда S = (T : 2) · 5 + (T : 2) · 3 = 4T (первую половину времени, то есть T : 2, он идёт со скоростью 5 км/ч и проходит расстояние (T : 2) · 5, а вторую половину времени, то есть тоже T : 2, он идёт со скоростью 3 км/ч и проходит расстояние (T : 2) · 3), откуда его средняя скорость равна S : T = 4 км/ч. Второй пешеход проходит то же расстояние за время t = (S : 2) : 3+(S : 2) : 5 = 4S : 15 (первую половину пути, то есть S : 2, он пройдёт со скоростью 3 км/ч за время (S : 2) : 3, а вторую половину времени, то есть тоже S : 2, он пройдёт со скоростью 5 км/ч за время (S : 2) : 5), откуда его средняя скорость равна S : t = 15/4 км/ч, что меньше 4 км/ч. Так что первый пешеход в среднем идет быстрее и поэтому придет в деревню раньше.

6.

Есть девять одинаковых на вид проб: пять проб золота и четыре пробы пирита («золота дураков»), лежащие в ящике по кругу. Известно, что никакие две пробы пирита не лежат рядом. Все пробы золота весят одинаково, и все пробы пирита — одинаково, но меньше, чем пробы золота. За два взвешивания на чашечных весах без гирек определите все пробы золота.

Решение

Решение.

Ясно, что пробы должны быть расположены по кругу в таком порядке: (G)old, (P)yrite, G, P, G, P, G, P, G (иначе две пробы Р окажутся рядом). Нужно только определить, где лежат рядом две пробы золота.

Пронумеруем пробы по часовой стрелке от 1 до 9. Сначала взвесим тройки (1, 2, 3) и (4, 5, 6). Если они уравновесились, то состав каждой из них {G, G, P} (в каком-то порядке), а (7, 8, 9) = (P,G,P) (именно в таком порядке, иначе две пробы Р окажутся рядом). Тогда 1 = G, 6 = G. Тогда вторым взвешиванием сравним пробы 2 и 5. Если они уравновесились, то это две пробы Р (если бы это были жве пробы G, то 3 и 4 — пробы Р, лежащие рядом, чего быть не может), если нет &mdahs; определяем, какая из них какая. После этого расположение остальных проб восстанавливается однозначно.

Если же при первом взвешивании оказалась тяжелее, скажем, тройка (1, 2, 3), то в этой тройке элементы {G, G, P} (в каком-то порядке), а (4, 5, 6) = (P, G, P) (именно в таком порядке, иначе две пробы Р окажутся рядом). Значит, среди проб 7, 8, 9 две пробы G и одна проба Р. Тогда вторым взвешиванием сравниваем пробы 1 и 9. Если они уравновесились, то это две пробы G (потому что две пробы Р не могут лежать рядом), если нет, то определяем, какая из них какая. Заметим ещё, что поскольку 6 = Р, может быть только 7 = G; поскольку 4 = Р, может быть только 3 = G. После этого расположение остальных проб восстанавливается однозначно.

7.

В стране есть несколько аэропортов, каждый из которых соединён авиалиниями ровно с пятью другими. Однажды из-за сильного снегопада бóльшую часть аэропортов пришлось закрыть. После этого оказалось, что из каждого работающего аэропорта можно вылететь только в три других, а закрытыми оказались 26 авиалиний. (Авиалиния закрывается, если закрывается хотя бы один из двух аэропортов, которые она соединяет.)

а)

Докажите, что число работающих после снегопада аэропортов чётно.

б)

Докажите, что число закрывшихся аэропортов делится на 4.

в)

Сколько авиалиний не закрылось из-за снегопада?

г)

Изменится ли ответ в пункте (в), если слова «бóльшую часть аэропортов» в условии заменить на «некоторые аэропорты»?

Ответ Решение

Ответ. в) 9; г) нет.

Решение.

а) Если работающих аэропортов n, то работающих авиалиний n · 3 : 2 (вспомните решение задачи 3). Чтобы это число было целым, n должно быть чётным.

б) Закрытые авиалинии — это те, которые соединяют пары из двух закрытых аэропортов и те, которые соединяют один работающий аэропорт и один закрытый. Если закрытых аэропортов m, то всех авиалиний было 5(m + n) : 2 (вспомните решение задачи 3), а закрылось после снегопада 5(m + n) : 2 − n · 3 : 2 = (5m + 2n) : 2 = 26, откуда 5m + 2n = 52 и 5m = 52 − 2n. В правой части этого уравнения число 52 делится на 4, а по пункту (а) число n чётно, поэтому 2n тоже делится на 4, так что правая часть делится на 4. Значит, и левая часть уравнения должна делиться на 4, поэтому m делится на 4.

в) Перебираем всевозможные натуральные m, кратные 4. Подходят только m = 4 (тогда из уравнения найдём n = 16) и m = 8 (тогда n = 6). При других m число n получается отрицательным. Условию удовлетворяет только второй из этих вариантов. Тогда, пользуясь рассуждениями из пункта (а), найдём, что не закрылось n · 3 : 2 = 6 · 3 : 2 = 9 авиалиний.

г) Если бы открытых аэропортов было 16 и каждый из них был соединён авиалиниями с двумя закрытыми, то закрытых авиалиний было бы не менее 16 · 2 = 32, что противоречит условию. Поэтому даже без условия о том, что закрылось бóльшая часть аэропортов, возможен только вариант m=8, n=6. Ответ от этого не изменится.